Giải câu 4 đề 18 ôn thi toán lớp 9 lên 10

Bài 4: (3,5 điểm)

Cho đường tròn tâm O, đường kính AB = 2R. Trên đường tròn (O) lấy điểm C bất kì (C không trùng với A và B). Tiếp tuyến của đường tròn (O) tại A cắt tia BC ở điểm D. Gọi H là hình chiếu của A trên đường thẳng DO. Tia AH cắt đường tròn (O) tại điểm F (không trùng với A). Chứng minh:

a.

b. Tứ giác AHCD nội tiếp

c.

d.

Bài làm:

Hình vẽ:

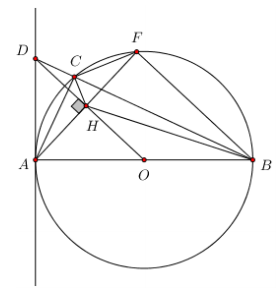
a.

Ta có: (góc nội tiếp chắn nửa đường tròn tâm O) => AC vuông góc BC hay AC vuông góc BD.

Ta có: (Do DA là tiếp tuyến của đường tròn tâm O tại A)

Áp dụng hệ thức lượng trong tam giác vuông ABD vuông tại A có đường cao AC ta có:

b.

Xét tứ giác AHCD có AHD=ACD= => Hai đỉnh C và H kề nhau cùng nhìn cạnh AD dưới góc => Tứ giác AHCD nội tiếp (tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh dưới các góc bằng nhau).

c. Do tứ giác AHCD nội tiếp nên = $\widehat{ADC}$ (cùng bù với $\widehat{AHC}$)

Xét tam giác FHC và tam giác ADC có:

= $\widehat{DAC}$ (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC)

= $\widehat{ADC}$ (cmt).

=> (hai góc tương ứng)

Mà = 90^{0}\Rightarrow $\widehat{FCH}$=90^{0}\Rightarrow CH\perp CF$

d. Xét tam giác vuông OAD vuông tại A có OH là đường cao ta có (hệ thức lượng trong tam giác vuông).

Mà

Xét tam giác OBH và ODB có:

chung;

(cmt)

Mà (hai góc nội tiếp cùng chắn cung CH của đường tròn ngoại tiếp tứ giác AHCD).

(hai góc nội tiếp cùng chắn cung CF của đường tròn (O)).

=>

Xét tam giác BHF và tam giác BAC có:

(góc BFC nội tiếp chắn nửa đường tròn (O)).

(cmt);