Các bài toán về số và chữ số dạng 2: Các bài toán giải bằng phân tích cấu tạo số

Chuyên đề 1: Các bài toán về số và chữ số dạng 2: Các bài toán giải bằng phân tích cấu tạo số. KhoaHoc sẽ hướng dẫn cụ thể và chi tiết các bước giải đối với dạng toán này nhằm giúp các em nắm rõ và có thể giải được các bài toán có dạng tương tự.

I. Ví dụ và hướng dẫn giải chi tiết

Loại 1. Viết thêm một số vào bên trái, bên phải hoặc xen giữa các chữ số của một số tự nhiên.

Ví dụ 1. Khi viết thêm số 36 vào bên phải một số tự nhiên có hai chữ số ta được một số mới gấp 102 lần số ban đầu. Tìm số có hai chữ số đó.

Giải.

Gọi số cần tìm là ab. Viết thêm số 36 vào bên phải số đó ta được số ab36.

Cách 1. Theo đề ra ta có :

ab36 = ab x 102

100 x ab + 36 = ab x 102

ab x 102 - ab x 100 = 36 (*)

ab x ( 102 - 100) = 36

ab x 2 = 36

ab = 36 : 2

ab = 18

Thử lại : 1836 : 18 = 102.

Cách 2. Sau khi phân tích đến bước (*) trong cách 1, ta có sơ đồ sau :

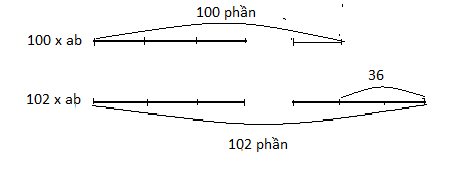
Dựa vào sơ đồ ta có số cần tìm là: 36 : ( 102 - 100) = 18.

Ví dụ 2. Khi thêm chữ số 12 vào bên trái số tự nhiên có hai chữ số thì số đó gấp lên 51 lần. Tìm số có hai chữ số đó.

Giải

Gọi số cần tìm là ab. Viết thêm số 12 vào bên trái ta được số 12ab.

Cách 1. Theo đề bài ta có:

12ab = ab x 51

1200 + ab = ab x 51

ab x 51 - ab = 1200

ab x (51 - 1) = 1200

ab x 50 = 1200

ab = 24

Cách 2. Sau khi phân tích đến bước (*) , ta có sơ đồ sau:

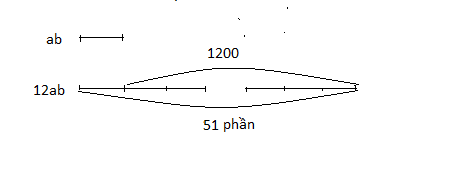
Dựa và sơ đồ ta thấy số cần tìm là:

1200 : (51 -1) = 24

Ví dụ 3. Tìm số tự nhiên có hai chữ số, biết rằng nếu viết thêm số 0 vào giữa chữ số hàng chục và hàng đơn vị thì số đó tăng lên 10 lần, nếu viết thêm chữ số 1 vào bên trái số vừa nhận được thì nó gấp lên 5 lần.

Giải

Gọi số cần tìm là ab. Khi viết thêm chữ số 0 vào giữa chữ số hàng chục và hàng đơn vị ta được số a0b.

Theo đề bài ta có:

ab x 10 = a0b

Vì ab x 10 có tận cùng là 0 nên b = 0. Vậy số cần tìm có dạng a0. Viết thêm chữ số 1 vào bên trái số a00 ta được số 1a00.

Theo đề bài ta có :

1a00 = 6 x a00

1000 + 100 x a = 600 x a

500 x a = 1000

a = 2

Vậy số cần tìm là 20.

Loại 2. Xoá đi một số chữ số của một số tự nhiên

Ví dụ 4. Khi xoá đi chữ số hàng chục và hàng đơn vị của một số tự nhiên có bốn chữ số thì số đó giảm đi 5544 đơn vị. Tìm số có bốn chữ số đó.

Giải. Gọi số cần tìm là abcd. Xoá đi chữ số hàng chục và hàng đơn vị ta được số ab.

Cách 1. Theo bài ra ta có :

abcd - ab = 5544

ab x 100 + cd - ab = 5544

cd + ab x (100 -1) = 5544

cd + ab x 99 = 5544

cd = 56 x 99 - ab x 99

cd = (56 - ab) x 99

Ta thấy cd là số bé hơn 100 do đó tích (45 -ab) x 99 là số bé hơn 100. Nên (56 - ab) bằng 0 hoặc 1

- Nếu 56 - ab = 0 thì ab = 56 và cd = 00.

- Nếu 56 - ab = 1 thì ab = 55 và cd = 99

Vậy số cần tìm là 5600 hoặc 5599.

Cách 2. Theo đề ra ta có : abcd - ab = 5544. Hay 5544 + ab = abcd

- Nếu cộng hàng chục không nhớ thì ab = 55 và abcd = 5544 + 55 = 5599.

- Nếu cộng hàng chục có nhớ thì ab = 55 + 1 = 56 và abcd = 5544 + 56 = 5600.

Vậy số cần tìm là 5600 hoặc 5599.

Ví dụ 5. Khi xoá đi chữ số hàng trăm của một số tự nhiên có ba chữ số thì số đó giảm đi 11 lần. Tìm số có ba chữ số đó.

Giải. Gọi số cần tìm là abc. Xoá đi chữ số hàng trăm ta được số bc.

Cách 1. Theo đề bài ta có :

abc = 11 x bc

a00 + bc = 11 x bc

a00 = (11 - 1) x bc

a00 = 10 x bc

a00 = bc0

Từ đó ta thấy c = 0 và a = b. Mà a khác 0 nên ta có các số thoả mãn đề bài là 110; 220; 330; 440; 550; 660; 770; 880; 990.

Cách 2. Ta có : abc = bc x 11

Hay abc = b(b+c)c

Từ đó ta thấy a = b và b = b + c.

Từ b = b + c ta có c = 0.

Vì a = b (a khác 0) nên ta có các số thoả mãn đề bài là 110; 220; 330; 440; 550; 660; 770; 880; 990.

Loại 3. Các bài toán về số tự nhiên và tổng các chữ số của nó.

Ví dụ 6. Tìm một số tự nhiên có hai chữ số, biết rằng số đó gấp 6 lần tổng các chữ số của nó.

Giải.

Cách 1. Gọi số cần tìm là ab. Theo đề ra ta có:

ab = 6 x (a +b)

10 x a + b = 6 x a + 6 x b

10 x a - 6 x a = 6 x b - b

(10 - 6) x a = (6 - 1) x b

4 x a = 5 x b

Từ đó suy ra a chia hết cho 5. Vậy a bằng 0, a bằng 5. Mà a khác 0 nên a = 5.

Khi đó b = 4.

Vậy số cần tìm là 54.

Loại 4. Các bài toán về số tự nhiên và hiệu các chữ số của nó

Ví dụ 7. Tìm một số có hai chữ số biết rằng số đó chia cho hiệu các chữ số của nó được thương là 24 và dư 2.

Giải. Gọi số cần tìm là ab và hiệu các chữ số của nó là c (c khác 0).

Theo đề ra ta có ab = 24 x c + 2.

Vì ab < 100 nên 24 x c + 2 < 100

Hay 24 x c < 98

Do đó c < 4. Vậy c bằng 1; 2 hoặc 3.

Nếu c = 1 thì ab = 26. Thử lại:6 - 2 = 4; 26 : 4 = 6 dư 2 (loại).

Nếu c = 2 thì ab = 50. Thử lại:5 - 0 = 5; 50 : 5 = 10 dư 0 (loại).

Nếu c = 3 thì ab = 74. Thử lại:7 - 4 = 3; 74 : 3 = 24 dư 2.

Vậy số cần tìm là 74.

Loại 5. Các bài toán về số tự nhiên và tích các chữ số của nó

Ví dụ 8. Tìm một số tự nhiên có hai chữ số, biết rằng số đó gấp 11 lần tích của các chữ số của nó.

Giải.

Gọi số cần tìm là ab.

Theo đề ra ta có :

ab = 11 x a x b

Vì 11 x a x b chia hết cho 11 nên ab cũng chia hết cho 11. Mà ab < 100 nên ab bằng 11; 22; 33; 44; 55; 66; 77; 88; 99.

- ab = 11. Thử lại 11 = 11 x 1 x1.

- ab = 22. Thử lại 22 = 11 x 2 x 2 (loại).

- ab = 33. Thử lại 33 = 11 x 3 x 3(loại).

- ab = 44. Thử lại 44 = 11 x 4 x 4(loại).

- ab = 55. Thử lại 55 = 11 x 5 x 5(loại).

- ab = 66. Thử lại 66 = 11 x 6 x 6(loại).

- ab = 77. Thử lại 77 = 11 x 7 x 7(loại).

- ab = 88. Thử lại 88 = 11 x 8 x 8(loại).

- ab = 99. Thử lại 99 = 11 x 9 x 9(loại).

Vậy số cần tìm là 11.