Giải câu 4 đề 9 ôn thi toán lớp 9 lên 10

1 Đánh giá

Bài 4: (3,5 điểm)

Cho đường tròn (O;R) với dây cung AB không đi qua tâm. Lấy S là một điểm bất kì trên tia đối của tia AB (S khác A). Từ điểm S vẽ hai tiếp tuyến SC, SD với đường tròn (O;R) sao cho điểm C nằm trên cung nhỏ AB (C, D là các tiếp điểm). Gọi H là trung điểm của đoạn thẳng AB.

1. Chứng minh năm điểm C, D, H, O, S thuộc đường tròn đường kính SO

2. Khi SO= 2R, hãy tính độ dài đoạn thẳng SD theo R và tính số đo CSD.

3. Đường thẳng đi qua điểm A và song song với đường thẳng SC, cắt đoạn thẳng CD tại điểm K. Chứng minh tứ giác ADHK là tứ giác nội tiếp và đường thẳng BK đi qua trung điểm của đoạn thẳng SC.

4. Gọi E là trung điểm của đoạn thẳng BD và F là hình chiếu vuông góc của điểm E trên đường thẳng AD. Chứng minh rằng, khi điểm S thay đổi trên tia đối của tia AB thì điểm F luôn thuộc một đường tròn cố định.

Bài làm:

1. Ta có $OH\perp HS$ (tính chất trung điểm dây cung)

=> H nằm trên đường tròn đường kính SO

Ta có C, D là tiếp điểm nên $OC\perp SC$ , $OD\perp SD$

=> C, D nằm trên đường tròn đường kính SO.

2. Ta có OD = R; SO = 2R

Do đó $SD =\sqrt{SO^{2}-OD^{2}}=\sqrt{4R^{2}-R^{2}}=R\sqrt{3}$

Và ta có $OSD = 30^{0}$ (Cạnh đối diện bằng nửa cạnh huyền)

Tương tự, ta có SC = SD = $R\sqrt{3}$ , $OSC = 30^{0}$

Do đó, tam giác SCD cân và có $CSD = 60^{0}$

=> Tam giác SCD đều.

3. Hình vẽ:

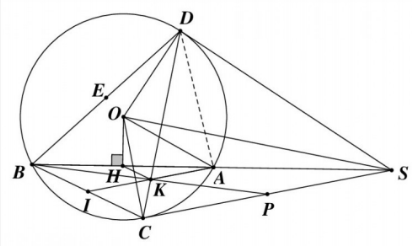
AK//SC nên AKD =SCD = ½ cung SD của đường tròn đường kính SO

Ta có SHD = 1/2 cung SD của đường tròn đường kính SO.

=>AKD =AHD=> Tứ giác ADHK nội tiếp.

Chứng minh BK đi qua trung điểm của SC

Gọi I là giao điểm của tia AK và đoạn thẳng BC, P là giao điểm tia BK và SC. Ta chứng minh K là trung điểm của AI, AI//SC từ đó suy ra BK đi qua trung điểm P của CS. (Dùng hệ quả định lí Ta-let).

4. Hình vẽ:

Gọi M là trung điểm OH, R là trung điểm OA, dễ chứng minh M cố ddonhj, MR là đường trung bình tam giác OAH, từ đó suy ra MR//HA, mà HA vuông góc OH => MR vuông góc OH=> $\angle OMR$ vuông.