Lời giải bài 3 chuyên đề Diện tích đa giác
Bài 3: Cho ![]() . Trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho $\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{3}$ . Gọi O là giao điểm của BN và CM.
. Trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho $\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{3}$ . Gọi O là giao điểm của BN và CM.
Gọi H, L lần lượt là chân đường vuông góc kẻ từ A, C tới đường thẳng BN.
a/ Chứng minh CL = 2 AH.
b/ Chứng minh: ![]() .
.
Kẻ CE và BD vuông góc với AO. Chứng minh BD = CE.
c/ Giả sử ![]() , tính $S_{AMON}$ .
, tính $S_{AMON}$ .
Bài làm:
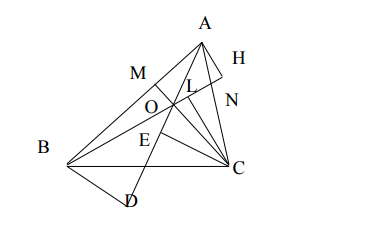
a/ Ta có : CN = 2 AN => ![]() (1)
(1)
BN là cạnh chung (2)
Từ (1) ,(2) => ![]()
Ta có : ![]()
![]() .
.
Và CL = 2AH . (đpcm).
b/ Từ câu (a) => ![]() . (*)
. (*)
Tương tự , ta có : ![]() (**)
(**)
Từ (*), (**) => ![]() (đpcm)
(đpcm)
Kẻ ![]() . (đpcm)
. (đpcm)
c/ Giả sử ![]() => $S_{BOA}=a (cm^{2})$
=> $S_{BOA}=a (cm^{2})$
![]()
=> ![]()
Mà theo giả thiết : ![]()
=> a = 5 (cm)
Mặt khác , ta có : ![]()
=> ![]() .
.
Xem thêm bài viết khác
- Đáp án đề thi vào lớp 10 môn Toán Hà Nội năm 2022 Đề thi môn Toán vào lớp 10 Hà Nội năm 2022
- Giải câu 5 đề 14 ôn thi toán 9 lớp 10
- Lời giải bài 1 chuyên đề Bài toán Dựng hình
- Đề thi tuyển sinh lớp 10 chuyên Toán tỉnh Hải Dương năm 2022 Đề thi vào 10 chuyên Toán Nguyễn Trãi, Hải Dương năm 2022
- Đề thi thử vào 10 môn Toán thành phố Hà Nội năm 2022 - Đề 21 Đề thi thử vào 10 môn Toán 2022
- Giải câu 3 đề 5 ôn thi toán lớp 9 lên 10
- Đề thi thử Toán vào 10 năm 2022 Đề thi thử Toán vào lớp 10
- Giải câu 4 đề 11 ôn thi toán lớp 9 lên 10
- Lời giải bài 4 chuyên đề Phương pháp đại số trong bài toán diện tích đa giác
- Đề ôn thi môn toán lớp 9 lên 10 (đề 6)
- Đáp án đề thi vào lớp 10 môn Toán Lai Châu năm 2022 Đề thi môn Toán vào lớp 10 tỉnh Lai Châu năm 2022
- Giải câu 4 đề 7 ôn thi toán lớp 9 lên 10











