[CTST] Giải SBT toán 6 bài 3: So sánh phân số

1 Đánh giá

Giải SBT toán 6 tập 2 bài 3: So sánh phân số sách "chân trời sáng tạo". KhoaHoc sẽ hướng dẫn giải tất cả câu hỏi và bài tập với cách giải nhanh và dễ hiểu nhất. Hi vọng, thông qua đó học sinh được củng cố kiến thức và nắm bài học tốt hơn.

Bài 1. So sánh hai phân số:

a) $\frac{-15}{1001}$ và $\frac{-12}{1001}$

b) $\frac{34}{-77}$ và $\frac{43}{-77}$

c) $\frac{77}{-36}$ và $\frac{-97}{45}$

Lời giải

a) $\frac{-15}{1001}$ < $\frac{-12}{1001}$

b) $\frac{34}{-77}$ > $\frac{43}{-77}$

c) $\frac{77}{-36}$ > $\frac{-97}{45}$

Bài 2. So sánh:

a) $\frac{501}{-101}$ và -5

b) -12 và $\frac{-145}{12}$

Lời giải

a) $\frac{501}{-101}$ > -5

b) -12 > $\frac{-145}{12}$

Bài 3. Sắp xếp các số theo thứ tự

a) tăng dần: -4; $\frac{10}{3}$ ; $\frac{9}{-2}$; và $\frac{-22}{-7}$;

b) giảm dần: $\frac{25}{-6}$ ; $\frac{-47}{-12}$; 4 và $\frac{-31}{8}$;

Lời giải

a) tăng dần: $\frac{9}{-2}$ ; -4; $\frac{-22}{-7}$; $\frac{10}{3}$

b) giảm dần: 4; $\frac{-47}{-12}$ ; $\frac{-31}{8}$; $\frac{25}{-6}$

Bài 4. Khẳng định sau đúng hay sai? Vì sao?

a) $\frac{-8}{15}<\frac{1}{-2}$

b) $\frac{-4}{3}>\frac{5}{-4}$

Lời giải

a) Đúng.

Vì $\frac{-8}{15}=\frac{-16}{30}$ và $\frac{1}{-2}=\frac{-15}{30}$

b) Sai

Vì $\frac{-4}{3}=\frac{-16}{12}$ và \frac{5}{-4}=\frac{-15}{12}$

Bài 5. Tìm số nguyên x thỏa mãn:

a) $\frac{-3}{7}<\frac{x}{7}<\frac{2}{7}$

b) $\frac{4}{-3}<\frac{x}{-3}<\frac{1}{3}$

Lời giải

a) $\frac{-3}{7}<\frac{x}{7}<\frac{2}{7}$

Phân số $\frac{x}{7}$ có cùng mẫu dương với hai phân số $\frac{-3}{7}$ và $\frac{2}{7}$

Do đó ta chỉ cần chọn số nguyên x sao cho -3 < x < 2

b) $\frac{4}{-3}<\frac{x}{-3}<\frac{1}{3}$

Ta đưa về bài toán tìm x sao cho $\frac{-4}{3}<\frac{-x}{-3}<\frac{1}{3}$

Xác định được -4 < -x < 1 nghĩa là -x có thể là một trong các số -3; -2; -1; 0

Từ đó suy ra x có thể là các số 3; 2; 1; 0

Bài 6. Một lớp học có nhiều học sinh yêu thích thể thao. Trong ngày hội thể thao của trường, lớp đã có $\frac{1}{2}$ số học sinh đăng kí thi đấu bóng đá, $\frac{2}{5}$ số học sinh đăng kí thi đấu bóng chuyền, $\frac{11}{20}$ số học sinh đăng kí thi đấu kéo co và $\frac{3}{10}$ số học sinh đăng kí thi đấu cầu lông. Hãy cho biết môn thi đấu nào được học sinh đăng kí nhiều nhất và môn thi đấu nào được học sinh đăng kí ít nhất (một học sinh có thể thi đấu nhiều môn)

Lời giải

Ta sắp xếp các phân số $\frac{1}{2}$ ; $\frac{2}{5}$; $\frac{11}{20}$; $\frac{3}{10}$ theo thứ tự tăng dần ta được:

$\frac{3}{10}$ ; $\frac{2}{5}$; $\frac{1}{2}$; $\frac{11}{20}$

Vậy môn thi đấu kéo co được đăng kí nhiều nhất, môn cầu lông đăng kí thi ít nhất

Bài 7. Quan sát thông tin trong cùng thời gian về nhiệt độ ở đỉnh Phan-xi-păng (Lào Cai, Việt Nam) và nhiệt độ ở Rovaniemi (Lapland, Phần Lan) trong hình sau và cho biết:

a) Số nhiệt độ trung bình trong ngày 28/12/2019 ở đỉnh Phan-xi-păng và ở Rovaniemi là hai phân số nào?

b) So sánh hai phân số ở câu a) và cho biết ý nghĩa thực tiễn của kết quả so sánh

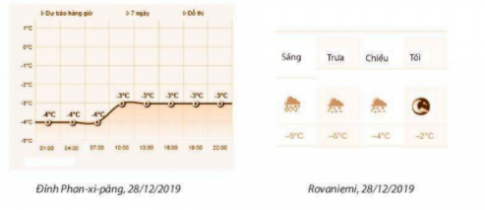
Lời giải

a) Từ thông tin có trong hình, ta thấy nhiệt độ trung bình ngày 28/12/2019 ở đỉnh Phan-xi-păng là trung bình cộng của nhiệt độ tại 8 thời điểm, còn nhiệt độ trung bình tại Rovaniemi là trung bình cộng tại 4 thời điểm. Phân số biểu thị nhiệt độ trung bình ở đỉnh Phan-xi-păng và Rovaniemi lần lượt là $\frac{-27}{8}$ và $\frac{-21}{4}$