Giải câu 4 trang 145 toán VNEN 8 tập 1

Câu 4: Trang 145 toán VNEN 8 tập 1

Cho hình thang ABCD có BC // AD và AB = BC = CD = a, AD = 2a. Gọi E là trung điểm của AD.

a) Tính theo a diện tích hình thang ABCD;

b) Tính theo a diện tích tứ giác ABCE;

c) Tính theo a diện tích tam giác ACD.

Bài làm:

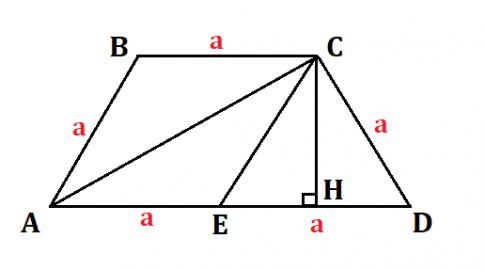
a) Kẻ đường cao CH với H thuộc AD.

Xét tứ giác ABCE có BC // AE và BC = AE (= a) nên ABCE là hình bình hành CE = a.

Xét tam giác CED có CE = CD (= a) nên CED cân tại C

CH vừa là đường cao, vừa là đường trung tuyến

H là trung điểm ED, hay EH = HD = $\frac{a}{2}$.

Áp dụng định lí Pi-ta-go vào tam giác CHD vuông tại H, có:

CH = = $\sqrt{a^2-{\frac{a}{2}}^2}$ = $\frac{a\sqrt{3}}{2}$.

Vậy S = $\frac{1}{2}$.(BC + AD).CH = $\frac{1}{2}$.(a + 2a).$\frac{a\sqrt{3}}{2}$ = $\frac{3a^2\sqrt{3}}{4}$ (đvdt).

b) S = CH.AE = $\frac{a\sqrt{3}}{2}$.a = $\frac{a^2\sqrt{3}}{2}$ (đvdt).

c) S = $\frac{1}{2}$.CH.AD = $\frac{1}{2}$.$\frac{a\sqrt{3}}{2}$.2a = $\frac{a^2\sqrt{3}}{2}$ (đvdt).