Lời giải bài 2 chuyên đề Diện tích đa giác

Bài 2: Cho có chu vi là 2p, cạnh BC = a, gọi góc $\widehat{BAC}=\alpha$ , đường tròn nội tiếp tam giác ABC tiếp xúc cạnh AC tại K.

Tính diện tích .

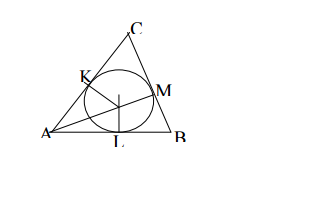
Bài làm:

Ta có : AK = AL; CK = CM; BM = BL

=> 2 CM + 2 AK + 2 BM = 2p .

Mà AK = p – (BM + CM) <=> AK = p – a

Vì theo giả thiết :

=>

+ OK = (p - a)

=> .