Lời giải bài 4 chuyên đề Bài toán Dựng hình

Bài 4: Cho một góc xOy và hai điểm A , B .Dựng một điểm cách đều hai cạnh Ox,Oy và cách đều hai điểm A , B.

Bài làm:

Phân tích bài toán :

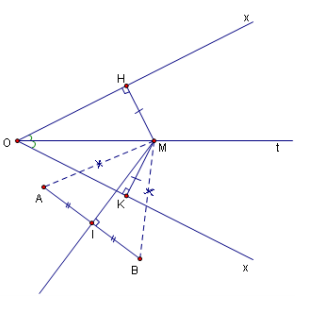
Giả sử bài toán đã giải xong và ta đã dựng được điểm M cách đều hai cạnh Ox, Oy và cách đều hai điểm A,B

Nghĩa là có MH = MK () và MA=MB.

Vậy M vưà thuộc tia phân giác Ot của xOy, vừa thuộc đường trung trực d của AB nên M là giao điểm của Ot và d .

Cách dựng hình :

Dựng tia phân giác Ot của góc xOy và đường trung trực d của AB ,d cắt Ot tại M.

=> M là điểm cần dựng.

Chứng minh:

Ta có :

• nên MH = MK .
• nên MA = MB.

Biện luận :

Ta có :

• d cắt Ot nếu AB không vuông góc với Ot => Bài toán có một nghiệm hình .
• Nếu và $OA \neq OB $ thì Ot // d => Bài toán vô nghiệm.
• Nếu và OA = OB thì $d \equiv Ot $ => Bài toán có vô số nghiệm,nghĩa là bất kỳ điểm nào của Ot cũng vừa cách đều hai cạnh Ox và Oy,vừa cách đều A và B.