Giải câu 4 đề 17 ôn thi toán 9 lên 10

Bài 4: (4,0 điểm)

Cho điểm C nằm ngoài đường tròn (O), kẻ hai tiếp tuyến CA, CB với đường tròn (O) (A, B là tiếp điểm).

a. Chứng minh 4 điểm C, A, O, B cùng thuộc một đường tròn

b. Vẽ dây AD // CO. CD cắt (O) tại E. Gọi giao điểm AE với CO là F. Chứng minh và $C{F}^2=FE.FA$

c. AB cắt CO tại H. Chứng minh ∠HEB = ∠CEF

d. Khi OC = 2R. Tính FO theo R.

Bài làm:

Hình vẽ:

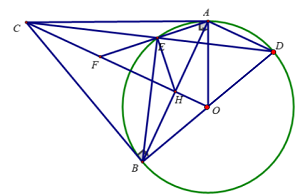
a. Xét tứ giác CAOB có:

∠CAO = (AC là tiếp tuyến của (O))

∠CBO = (BC là tiếp tuyến của (O))

=> ∠CAO + ∠CBO =

=> Tứ giác BCAO là tứ giác nội tiếp

b. Xét đường tròn (O) có:

∠CAF = ∠ADE (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn 1 cung)

Lại có: ∠ECF = ∠ADE (CO // AD; hai góc so le trong)

=> ∠CAF = ∠ECF

Xét ΔCFA và ΔEFC có:

∠CAF = ∠ECF

∠CFA là góc chung

=> ΔCFA ∼ ΔEFC

c. Ta có:

∠CAF = ∠EBA (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn 1 cung)

Lại có: ∠CAF = ∠ECF (cmt)

=> ∠EBA = ∠ECF

Xét tứ giác CEBH có:

∠EBA = ∠ECF

=> 2 đỉnh B và C cùng nhìn EH dưới 2 góc bằng nhau

=> Tứ giác CEBH là tứ giác nội tiếp

=> ∠BEH = ∠HCB ( 2 góc nội tiếp cùng chắn cung HB)

Mà ∠HCB = ∠HCA (CO là tia phân giác của góc ACB)

=> ∠BEH = ∠HCA (1)

Mặt khác: ΔCFA ∼ ΔEFC => ∠HCA = ∠CEF (2 góc tương ứng) (2)

Từ (1) và (2) : ∠BEH = ∠CEF

d. Xét tam giác ACO vuông tại A có:

=>

Ta có: AB ⊥ CO (Tính chất 2 tiếp tuyến cắt nhau)

CO // AD (gt)

=> AB ⊥ AD => BD là đường kính của đường tròn (O)

Xét tam giác BCD vuông tại B có:

=> CD = R√7

Xét ΔCEA và ΔCDA có:

là góc chung

=$\widehat{ADC}$ (2 góc cùng chắn một cung)

=>

Xét tam giác CAO vuông tại A có:

=> => $\angle AOD={60}^0$ (kề bù với góc (BOA )

Tam giác AOD cân tại O có ∠AOD = nên tam giác AOD đều

=> AD = AO = R

Ta có: OC // AD