Giải câu 4 đề 16 ôn thi toán lớp 9 lên 10

1 Đánh giá

Bài 4: (4,0 điểm)

Cho hình chữ nhật ABCD nội tiếp đường tròn tâm O. Tiếp tuyến của đường tròn tâm O tại điểm C cắt các đường thẳng AB và AD theo thứ tự tại M, N. Dựng AH vuông góc với BD tại điểm H, K là giao điểm của hai đường thẳng MN và BD.

a. Chứng minh tứ giác AHCK là tứ giác nội tiếp.

b. Chứng minh AD.AN = AB.AM.

c. Gọi E là trung điểm của MN. Chứng minh ba điểm A, H, E thẳng hàng.

d. Cho AB = 6cm, AD = 8cm. Tính độ dài đoạn MN.

Bài làm:

Hình vẽ:

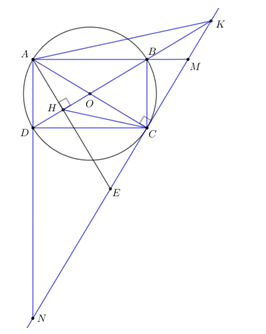
a. Xét tứ giác AHCK ta có: $\widehat{AHK}=\widehat{ACK}=90^{0}$

Mà hai đỉnh H,CH,C kề nhau cùng nhìn cạnh AK dưới góc $90^{0}$

⇒AHCK là tứ giác nội tiếp. (dhnb)

b. Chứng minh AD.AN = AB.AM.

Ta có: $AM//CD\Rightarrow \widehat{AMN}=\widehat{DCN}$ (hai góc đồng vị)

$\widehat{DCN}$ là góc tạo bởi tia tiếp tuyến và dây cung chắn cung CD.

$\widehat{ABD}$ là góc nội tiếp chắn cung AB.

Mà cung AB bằng cung CD do ABCD là hình chữ nhật.

$\Rightarrow \widehat{ADB}=\widehat{AMN}(=\widehat{DCN})$

Xét $\Delta ABD$ và $\Delta ANM$ ta có:

$\widehat{A}$ chung

$\widehat{ADB}=\widehat{AMN} (cmt)$

$\Rightarrow \Delta ABD\sim \Delta AMN (g.g)$

$\Rightarrow \frac{AB}{AN}=\frac{AD}{AM}\Rightarrow AB.AM=AD.AN (đpcm)$

c. Ta có E là trung điểm của MN(gt) ⇒ AE = ME = EN tính chất đường trung tuyến ứng với cạnh huyền).

$\Rightarrow \widehat{EAN}=\widehat{ENA}$

$\Rightarrow \widehat{AEM}=\widehat{EAN}+\widehat{ANE}=2\widehat{ENA}$ (góc ngoài của tam giác)

Vì $\Delta ABD\sim \Delta ANM (cmt)\Rightarrow \widehat{ABD}=\widehat{ANC}$ (hai góc tương ứng)

Vì ABCD là hình chữ nhật $\Rightarrow \widehat{ABD}=\widehat{BDC}$ (hai góc so le trong)

$\Rightarrow \widehat{BDC}=\widehat{ANC}(=\widehat{ABD})$

$\Rightarrow \widehat{HEC}=2\widehat{ANE}=2\widehat{BDC}=2\widehat{ODC}(1)$

Xét $\Delta OCD$ cân tại O ta có: $\widehat{DOC}+\widehat{OCD}+\widehat{ODC}=180^{0}$

$\Leftrightarrow \widehat{DOC}+2.\widehat{ODC}=180^{0}(2)$

$\Rightarrow \widehat{DOC}+\widehat{HEC}=180^{0}$

Từ (1) và (2) => $\widehat{DOC}+\widehat{HEC}=180^{0}$ (cmt)

Xét tứ giác OHEC ta có: $\widehat{DOC}+\widehat{HEC}=180^{2}(cmt)$

⇒OHEC là tứ giác nội tiếp (tổng hai góc đối diện có tổng bằng $180^{0}$ ).

$\Rightarrow \widehat{OHE}+\widehat{OCE}=180^{2}$

$\Leftrightarrow \widehat{OHE}=180^{2}-90^{2}=90^{2}$

$\Rightarrow OH\perp HE$

Mà $OE\perp AH (gt)$ => A, H, E thẳng hàng.

d. Áp dụng định lý Pi-ta-go cho tam giác ABC vuông tại A ta có:

$DB^{2}=AB^{2}+AD^{2}=6^{2}+8^{2}=10^{2}\Rightarrow BD=10cm$

Vì $\Delta ABD\sim \Delta ANM (cmt)$

$\Rightarrow \frac{AB}{AN}=\frac{BN}{MN}=\frac{AD}{AM}$

$\Leftrightarrow \frac{6}{AN}=\frac{8}{AM}=\frac{10}{MN}$

$\Leftrightarrow \left\{\begin{matrix}AM=\frac{8MN}{10}=\frac{4}{5}MN& & \\ AN=\frac{6}{10}MN=\frac{3}{5}MN& & \end{matrix}\right.$

Xét tam giác $\Delta DBC$ và $\Delta CMB$ ta có:

$\widehat{DCB}=\widehat{CBM}=90^{2}$

$\widehat{BDC}=\widehat{BCM}$ (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BC).

$\Rightarrow \Delta DCB\sim CBM (g-g)$

$\Rightarrow \frac{DC}{BC}=\frac{BC}{BM}\Leftrightarrow \frac{6}{8}=\frac{8}{BM}$

$\Leftrightarrow BM=\frac{32}{3}$ (cm)

$\Rightarrow AM= AB +BM = 6 + \frac{32}{3}=\frac{50}{3}$ (cm)

$\Rightarrow MN=\frac{5}{4}AM=\frac{5}{4}.\frac{50}{3}=\frac{125}{6}$ (cm)

Vậy $MN=\frac{125}{6}$ (cm)

3 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Ôn toán 9 lên 10