Lời giải Bài 1-Một số bài toán Hình học thường gặp trong đề tuyển sinh vào 10 năm 2017

Bài làm:

Lời giải chi tiết :

Đề ra :

Cho tam giác ABC có các đường cao BD , CE .Đường thẳng DE cắt đường tròn ngoại tiếp tam giác tại hai điểm M và N .

a. Chứng minh : BEDC nội tiếp .

b. Chứng minh : .

c. Chứng minh : DE // với tiếp tuyến tại A của đường tròn ngoại tiếp tam giác .

d. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC . Chứng minh OA là phân giác góc .

e. Chứng minh : .

Hướng dẫn giải :

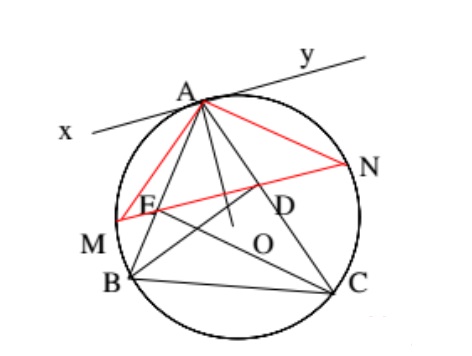
a.

Ta có :

=>

=> Tứ giác BEDC nội tiếp . ( đpcm )

b.

Do BEDC nội tiếp =>

Mà :

=> ( đpcm )

c.

Gọi tiếp tuyến tại A của (O) là đường thằng xy

=> xy cũng là đường tiếp tuyến .

Vì AB là dây cung => sđ góc = $\frac{1}{2}$ sđ cung AB .

Mặt khác , ta có : sđ góc = $\frac{1}{2}$ sđ cung AB .

=>

Mà :

=> hay xy // DE .

Vậy DE // với tiếp tuyến tại A của đường tròn ngoại tiếp tam giác . ( đpcm )

d.

Vì : xy // DE => xy // MN

Mà : => $OA\perp MN$

=> OA là đường trung trực của MN .

=> cân tại A .

=> AO là phân giác của góc . ( đpcm )

e.

Do : cân tại A => AM = AN

=> sđ cung AM = sđ cung AN

=>

Và :

=>

=> ( đpcm )