Lời giải Bài 7-Một số bài toán Hình học thường gặp trong đề tuyển sinh vào 10 năm 2017

Bài làm:

Lời giải chi tiết :

Đề ra :

Cho tam giác đều ABC nội tiếp trong ( O,R ) .Trên cạnh AB và AC lấy hai điểm M, N sao cho BM = AN .

a. Chứng tỏ : cân .

b. Chứng minh : OMAN nội tiếp .

c. BO kéo dài cắt AC tại D và cắt (O) tại E. Chứng minh : .

d. Đường thẳng CE và AB cắt nhau tại F. Tiếp tuyến tại A của (O) cắt FC tại I . AO kéo dài cắt BC tại J . Chứng minh : BI đi qua trung điểm của AJ .

Hướng dẫn giải :

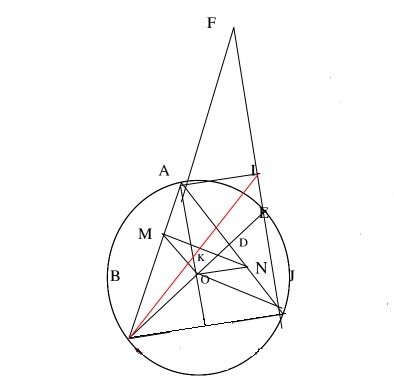
a.

Do là tam giác đều nội tiếp trong (O)

=> AO và BO là phân giác của .

=>

Mặt khác :

=>

=> cân . ( đpcm )

b.

Do :

Mà :

=>

=> Tứ giác OMAN nội tiếp . ( đpcm )

c.

Do BO là phân giác của đều => $BO\perp AC$

=> vuông tại D .

Áp dụng hệ thức Py-ta-go , ta có :

<=>

Mà : OB = R

Xét cân tại O , có : $\widehat{OAC}=30^{\circ}$

=>

=>

=> là tam giác đều => $AD\perp OE=> OD=ED=\frac{R}{2}$

Áp dụng Py-ta-go , ta có : (2)

Từ (1), (2) =>

Vậy ( đpcm )

d.

Gọi K là giao điểm của BI và AJ .

Ta có :

• ( góc nội tiếp chắn nửa đường tròn )
• 
• 

=>

Do :

=> AI // BC .

Mà A là trung điểm BF => I là trung điểm CF .

<=> FI = IC . (*)

+ Vì AK // FI . Áp dụng hệ quả định lý Talet trong tam giác BFI , ta có :

+ Vì KJ // CI . Áp dụng hệ quả định lý Talet trong tam giác BIC , ta có :

=>

Từ (*) => AK = KJ . ( đpcm )

Vậy BI đi qua trung điểm của AJ .