Lời giải Câu 4 Đề thi thử lên lớp 10 môn toán năm 2017 của trường THPT Chu Văn An

Bài làm:

Lời giải câu 4 :

Đề bài :

Cho đường tròn tâm O, dây cung AB cố định (AB không phải là đường kính của đường tròn). Từ điểm M di động trên cung nhỏ AB (), kẻ dây cung MN vuông góc với AB tại H. Từ M kẻ đường vuông góc với NA cắt đường thẳng NA tại Q.

a) Chứng minh bốn điểm A, M, H, Q nằm trên một đường tròn. Từ đó suy ra MN là tia phân giác của góc BMQ.

b) Từ M kẻ đường thẳng vuông góc với NB cắt NB tại P. Chứng minh .

c) Chứng minh ba điểm P, H, Q thẳng hàng.

d) Xác định vị trí của M trên cung AB để ( MQ.AN + MP.BN ) có gía trị lớn nhất.

Hướng dẫn giải chi tiết :

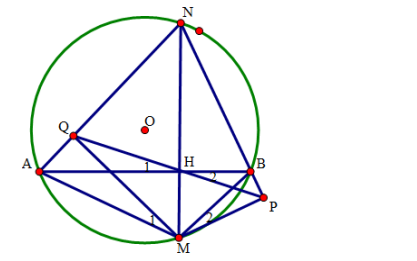
a. Ta có : (cùng chắn cung QH)

<=>

Mà (cùng chắn cung NB)

=>

Vậy MN là tia phân gíac của BMQ

b. Ta có: (cùng chắn cung MB)

=>

Mà

=>

c. Ta có: (cùng chắn cung AQ)

Vì tứ giác AHBP nội tiếp nên (cùng chắn cung BP)

Và => $\widehat{AHQ}=\widehat{PHB}$

Mặt khác : vì ba điểm A, H, B thẳng hàng => ba điểm P, H, Q thẳng hàng.

Vậy ba điểm P, H, Q thẳng hàng.

d. Ta có: MQ.AN + MP.BN = 2() = MN.AH + MN.BH = MN.AB

Vì AB không đổi nên MQ.AN + MP.BN có giá trị lớn nhất khi MN lớn nhất

<=> MN là đường kính => M nằm chính giữa cung nhỏ AB.

Vậy M nằm chính giữa cung nhỏ AB thì ( MQ.AN + MP.BN ) có gía trị lớn nhất.