Lời giải bài 3 chuyên đề Bài toán Dựng hình

Bài 3: Cho một góc xOy và một điểm M ở bên trong góc ấy .Dựng một đoạn thẳng AB sao cho và M là trung điểm của AB.

Bài làm:

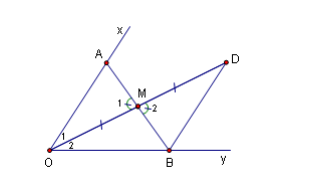
Phân tích bài toán :

Giả sử bài toán giải xong và ta đã dựng được đoạn thẳng AB thoả mãn yêu cầu của đề bài là và M là trung điểm của AB.

Nếu kéo dài OM thêm đoạn MD = OM thì (c.g.c)

=>

Từ đó , DB // Ox .

Ngược lại, nếu từ D kẻ DB // Ox ( ) ,rồi BM đến cắt Ox tại A thì $\mathrm{△}AMO=\mathrm{△}BMD$ (g.c.g)$ với :

• (đối đỉnh)
• (so le trong ,DB // Ox)
• MD = OM (do dựng )

=> AM = MB.

Cách dựng hình :

Kéo dài OM thêm đoạn MD= OM ,rồi từ D kẻ đường thẳng // Ox ,cắt Oy tại B.

Tiếp đến kẻ BM cho đến cắt Ox tại A thì M là trung điểm của AB.

Chứng minh:

Xét và $\mathrm{△}BMD$ có :

• (đối đỉnh)
• MD = OM (do dựng )
• (so le trong ,DB // Ox)

=> (g.c.g)$

=> AM = MD .

Biện luận :

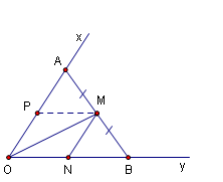
Bài toán luôn có một nghiệm.

* Bài toán có thể phân tích cách khác : Kéo MN // Ox ( ) => MN= 2 OA .

Ngược lại, nếu kẻ MN // Ox ( ),và lấy điểm A trên Ox sao cho OA = 2MN ,rồi kẻ AM đến cắt Oy tại B thì có AM =MB.

Quả vậy ,gọi B là trung điểm của OA => OP = PA => PM // ON.

Vậy BM phải đi qua trung điểm của AB,tức AM = MB .

Qua phân tích này ta thấy rõ cách dựng và chứng minh .

Vậy bài toán luôn có một nghiệm.