Lời giải Bài 3 Đề thi thử lên lớp 10 môn toán lần 1 năm 2017 của trường THPT chuyên Nguyễn Huệ

Bài làm:

Lời giải bài 3 :

Đề bài :

Cho hình chữ nhật ABCD nội tiếp đường tròn tâm O, bán kính R, có .

a) Tính các cạnh của hình chữ nhật ABCD theo R.

b) Trên cung nhỏ BC lấy điểm M ( ). Gọi G là trọng tâm của tam giác MBC. Khi điểm M di động trên cung nhỏ BC thì điểm G di động trên đường nào?

Hướng dẫn giải chi tiết :

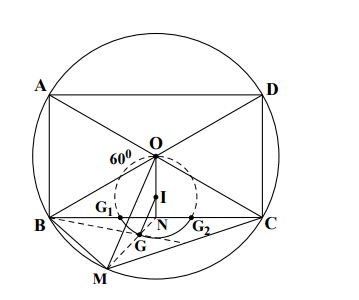
a. Theo giả thiết ta có :

+

=> AB = CD = R (AB là cạnh của lục giác đều nội tiếp) .

+

=> AD = BC = (AD là cạnh của tam giác đều nội tiếp) .

b. Gọi N là trung điểm của BC và I thuộc NO sao cho <=> I và N cố định.

Do G là trọng tâm của ΔMBC nên: .

Mà

=>

=>

<=>

=> Điểm G thuộc đường tròn tâm I, bán kính = .

Giới hạn :

+ Khi

+ Khi ( với $G_{1},G_{2}$ là giao điểm của đường tròn (I) với BC và $NG_{1}=\frac{1}{3}NB;NG_{2}=\frac{1}{3}NC$ )

Vậy khi điểm M di động trên cung nhỏ BC thì điểm G di động trên cung của đường tròn $(I;\frac{1}{3}R)$ .