Lời giải Bài 4 Đề thi thử lên lớp 10 môn toán lần 2 năm 2017 của trường THPT chuyên TP HCM

Bài làm:

Lời giải bài 4 :

Đề bài :

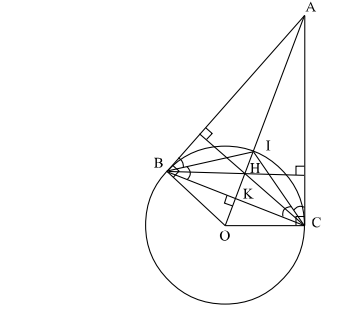
Cho đường tròn tâm O và điểm A nằm ngoài đường tròn . Từ A kẻ hai tiếp tuyến AB , AC với đường tròn ( B, C là hai tiếp điểm ).

a. Chứng minh tứ giác ABOC nội tiếp .

b. Gọi là trực tâm tam giác ABC , chứng minh tứ giác BOCH là hình thoi .

c. Gọi I là giao điểm của đoạn thẳng OA với đường tròn .Chứng minh I là tâm đường tròn nội tiếp tam giác ABC .

d. Cho OB = 3 cm , OA = 5 cm . Tính diện tích tam giác ABC .

Hướng dẫn giải chi tiết :

a.

Ta có :

=>

Vậy tứ giác ABOC nội tiếp . (đpcm)

b. Ta có : (1)

Tương tự : OC // BH (2)

Từ (1),(2) => OBHC là hình bình hành .

Mặt khác : OB = OC

=> OBHC là hình thoi .

c. Vì I là giao điểm của đoạn thẳng OA với đường tròn => I là điểm chính giữa cung BC.

Ta có : OA là đường phân giác (1)

Mặt khác :

Và

=>

=> BI là đường phân giác (2)

Từ (1) , (2) => I là tâm đường tròn nội tiếp tam giác ABC . (đpcm)

d. Gọi K là giao điểm của OA và BC

=> K là trung điểm của BC <=> KB = KC .

Áp dụng định lí Py-ta-go cho tam giác vuông AOB , ta có :

<=> AB = 4 .

Áp dụng hệ thức lượng tam giác vuông ABO , ta có :

=>

Ta có :

=>

Vậy .