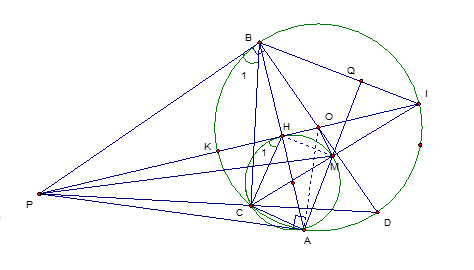
Lời giải Bài 4 Đề thi thử lên lớp 10 môn toán lần 3 năm 2017 của Trường THPT chuyên Vinh

Bài làm:

Lời giải bài 4:

Đề bài :

Cho đường tròn (O) và một điểm P ở ngoài đường tròn. Kẻ hai tiếp tuyến PA, PB với đường tròn (O) (A ,B là hai tiếp điểm). PO cắt đường tròn tại hai điểm K và I ( K nằm giữa P và O) và cắt AB tại H. Gọi D là điểm đối xứng của B qua O, C là giao điểm của PD và đường tròn (O).

a. Chứng minh tứ giác BHCP nội tiếp.

b. Chứng minh .

c. Đường tròn ngoại tiếp tam giác ACH cắt IC tại M. Tia AM cắt IB tại Q. Chứng minh M là trung điểm của AQ.

Hướng dẫn giải chi tiết :

a. Xét , ta có:

• PA = PB.
• ( tính giất hai tiếp tuyến cắt nhau ) .

=> cân tại P và PO là phân giác .

=> PO cũng là đường cao, trung tuyến của .

Xét tứ giácBHCP , ta có :

• ( vì $PO\perp AB$ ) .
• ( vì kề bù $\widehat{BCD}=90^{\circ}$ ( nội tiếp nửa đường tròn (O) ) .

=> Tứ giác BHCP nội tiếp ( Qũy tích cung chứa góc ) .

b. Xét , ta có :

• ( chắn cung $\widehat{BKC}$ của đường tròn (O))
• ( do BHCP nội tiếp )

=>

Mà : ( vì $PO\perp AB$ )

=>

=> vuông tại C <=> $AC\perp CH$ . ( đpcm )

c. Xét tứ giác ACHM , ta có : M nằm trên đường tròn ngoại tiếp )

=> Tứ giác ACHM nội tiếp .

=> (chắn cung HC )

Mà (chắn cung BC của đường tròn (O))

=>

=> MH // BI ( vì cặp góc đồng vị bằng nhau ) .

Xét , ta có :

AH = BH ( do PH là trung tuyến )

MH // BI ( c/m trên )

=> MH là đường trung bình .

=> M là trung điểm của AQ . ( đpcm )