Lời giải Bài 3 Đề thi thử lên lớp 10 môn toán lần 1 năm 2017 của trường THPT chuyên Sư Phạm Hà Nội

Bài làm:

Lời giải bài 3 :

Đề bài :

Cho tam giác ABC không tù, có đường cao AH và tia phân giác trong BD của cắt nhau tại E ($H\in BC;D\in AC$ ) sao cho AE = 2EH và BD = 2AE. Chứng minh rằng tam giác ADE đều.

Hướng dẫn giải chi tiết :

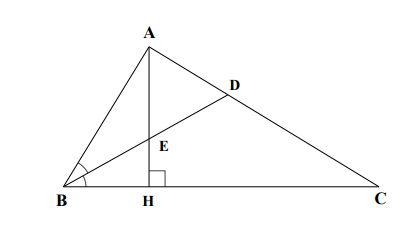
Ta có BE là phân giác của nên $\frac{EH}{EA}=\frac{BH}{BA}$

Mà AE = 2EH ( gt) =>

Xét có : $\cos \widehat{B}=\frac{BH}{BA}=\frac{1}{2}=>\widehat{B}=60^{\circ} $

=>

(1)

=> cân tại E => AE = BE .

Mà BD = 2AE (gt) => AE = DE => cân. (2)

Từ (1), (2) => đều (đpcm ).