Lời giải Bài 4 Đề thi thử lên lớp 10 môn toán lần 2 năm 2017 của Trường THPT chuyên Thái Bình

Bài làm:

Lời giải bài 4 :

Đề ra :

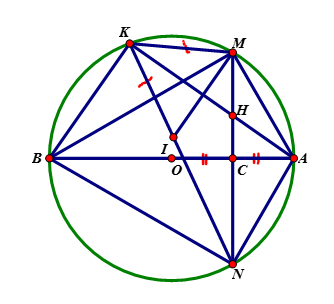
Cho đường tròn tâm O đường kính AB = 2R. Gọi C là trung điểm của OA; qua C kẻ đường thẳng vuông góc với OA cắt đường tròn đó tại hai điểm phân biệt M và N. Trên cung nhỏ BM lấy điểm K ( K khác B và M), trên tia KN lấy điểm I sao cho KI = KM. Gọi H là giao điểm của AK và MN. Chứng minh rằng:

a. Tứ giác BCHK là tứ giác nội tiếp.

b. AK.AH = R^{2 .}

c. NI = BK .

Lời giải chi tiết:

a. Ta có : ( góc nội tiếp chắn nửa đường tròn ) .

=> Tứ giác BCHK nội tiếp .

b. Ta có : ( g-g )

=>

Mà : AB = 2R => (1)

C là trung điểm của AO => (2)

=> ( đpcm ) .

c. Ta có: đều (cân tại M và O) .

=>

=> là những tam giác đều .

Xét và $\triangle IMN $ có:

• MK = MI ( cạnh tam giác đều KMI ) .
• ( cùng cộng với góc BMI bằng 60⁰ )
• MB = MN ( cạnh tam giác đều BMN )

=> ( c-g-c ) .

=> NI = BK . ( đpcm )