Lời giải Bài 4 Đề thi thử lên lớp 10 môn toán lần 4 năm 2017 của Trường chuyên Lam Sơn Thanh Hóa

Bài làm:

Lời giải bài 4 :

Đề bài :

Cho tứ giác ANPQ nội tiếp (O) đường kính AQ .Hai đường chéo AP và NQ cắt nhau tại E . Gọi F là điểm thuộc AQ sao cho EF vuông góc với AQ .Đường thẳng PF cắt (O) tại điểm thứ hai là K .NQ và PF cắt nhau tại L .Chứng minh rằng :

a. Tứ giác PEFQ nội tiếp .

b. FM là tia phân giác của góc NFM.

c. NE.QL = QN.EL .

Hướng dẫn giải chi tiết :

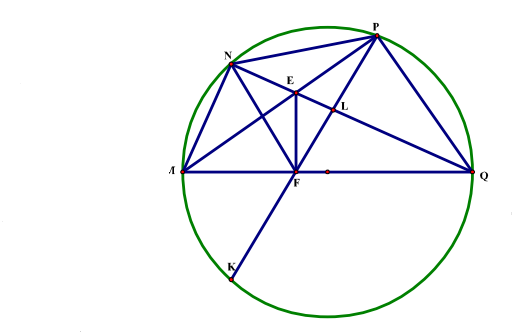
a. Ta có :

( góc nội tiếp chắn nửa đường tròn )

=> Tứ giác PEFQ nội tiếp ( đpcm ) .

b. Ta có :

=> Tứ giác MNEF nội tiếp .

=> ( 2 góc nội tiếp cùng chắn cung PQ trong đường tròn đường kính EQ )

( 2 góc nội tiếp cùng chắn cung MN trong đường tròn đường kính ME )

( 2 góc đối dỉnh )

( 2 góc đối đỉnh )

=> hay PM là tia phân giác của góc NFM .

Vậy PM là tia phân giác của góc NFM . ( đpcm )

c. Ta có :

( 2 góc nội tiếp cùng chắn cung MN trong đường tròn đường kính MQ )

( 2 góc nội tiếp cùng chắn cung EF trong đường tròn đường kính EQ )

=>

=> PE là phân giác trong của . (1)

Mà : => PE là phân giác ngoài của $\triangle NPL$ . (2)

Từ (1) , (2) => ( đpcm ) .