Lời giải bài 5 chuyên đề Bài toán Dựng hình

Bài 5: Cho một góc nhọn xOy và một điểm A trên Oy.Tìm một điểm M trên đoạn OA sao cho nếu kẻ MP = MA.

Bài làm:

Phân tích bài toán :

Giả sử bài toán đã giải xong và ta đã dựng được điểm M theo yêu cầu của đề bài.

Kẻ PN // AM và PN = AM => AN // NP , Có nghĩa là (1)

Mặt khác PN = AM = OP nên tam giác OPN cân :

Mà (góc so le trong PN // Oy) => $\widehat{O_1}=\widehat{O_2}$.

Điều đó có nghĩa là N nằm trên tia phân giác của góc xOy .

Theo (1) thì N nằm trên đường thẳng vuông góc với Ox hạ từ A.Vậy N là giao điểm của đường thẳng đó với tia phân giác của góc xOy . Vị trí N hoàn toàn xác định => do đó dựng được hình theo yêu cầu.

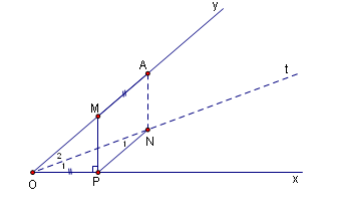
Cách dựng hình :

Kẻ tia phân giác Ot của góc xOy và từ A ,kẻ đường thẳng vuông góc với Ox , cắt Ot tại N .

Từ N kẻ NP // Oy ,cắt Ox tại P .Từ P kẻ đường thẳng vuông góc với Ox, cắt Oy tại điểm N cần dựng .

Chứng minh :

Ta có :

NP // Oy nên (so le trong )

Mà Ot là tia phân giác : .

=>

=> Tam giác OPN cân tại P : OP = PN.

Mà MP và AN cùng vuông góc với Ox nên MP // AN

=> PN = AM (đoạn thẳng song song bị chắn bởi hai đƣờng thẳng song song) (2)

Từ (1),(2) => OP = AM.

Biện luận:

Góc xOy nhọn nên tia phân giác Ot cắt đường thẳng kẻ từ A vuông góc với Ox tại một điểm N duy nhất.Do đó bài toán có một nghiệm hình như hình vẽ.