Đáp án câu 4 đề 2 kiểm tra học kì 2 Toán 9

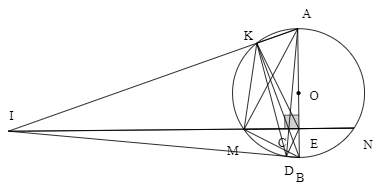
Câu 4(4,5 điểm): Cho đường tròn (O;R), dây MN cố định (MN < 2R). Kẻ đường kính AB vuông góc với dây MN tại E. Lấy điểm C thuộc dây MN (C khác M, N, E), BC cắt đường tròn (O) tại điểm K (K khác B).

a, Chứng minh: Tứ giác AKCE nội tiếp được một đường tròn.

b, Chứng minh: = BK.BC

c, Gọi I là giao điểm của AK và MN; D là giao điểm của AC và BI

+ Chứng minh: D thuộc (O;R)

+ Chứng minh điểm C cách đều ba cạnh của ∆DEK

Bài làm:

a, Xét đường tròn (O) có: (góc nội tiếp chắn nửa đường tròn)

Ta có tại E $\Rightarrow \widehat{AEM}=\widehat{BEM}={90}^{\circ }$

Xét tứ giác AKCE có

$\Rightarrow tứ giác AKCE nội tiếp được một đường tròn.

b, Xét đường tròn (O) có : AB là đường kính, MN là dây và .

B là điểm chính giữa cung MN $\Rightarrow$ hai cung BM và BN bằng nhau.

(2 góc chắn 2 cung bằng nhau).

Xét ∆BMC và ∆BKM có: chung và $\widehat{MKB}=\widehat{CMB}$

∆BMC $\sim$ ∆BKM (g.g)

= BK.BC

c,

+, Xét ∆AIB có BK, IE là hai đường cao

Mà BK ∩ IE = {C} => C là trực tâm của ∆AIB

AC là đường cao của ∆AIB

hay $AD\perp IB\Rightarrow \widehat{ADB}={90}^{\circ }$

D thuộc đường tròn đường kính AB.

Hay D thuộc (O; R).

+, (góc nội tiếp chắn nửa đường tròn)

(2 góc nội tiếp cùng chắn cung CE )

Mà (2 góc nội tiếp cùng chắn cung AK của (O))

Do đó DC là tia phân giác của $\widehat{KDE}$

Chứng minh tương tự ta có KC là tia phân giác của

Do đó C là tâm đường tròn nội tiếp ∆DKE

Vậy C cách đều 3 cạnh của ∆DKE.