Đáp án đề 1 kiểm tra cuối năm toán 6

1. Tính: A =

2. Tìm x, biết:
a.

b.

3. Tìm x , biết: $\frac{1}{2}+\frac{1}{3}-2\frac{1}{5}\leq x< 4\frac{1}{5}+3\frac{1}{2}$

4. Hai vòi nước cùng chảy vào một cái bể. Vòi thứ nhất chảy riêng trong 6 giờ thì đầy bể; vòi thứ hai chảy riêng trong 8 giờ thì đầy bể . Người ta mở vòi thứ nhất chảy riêng trong 1 giờ 15 phút và khóa lại, sau đó mở vòi hai. Hỏi vòi thứ hai phải chảy tiếp trong bao lâu mới đầy bể ?

5. Cho ba đường thẳng xx', yy', zz' cắt nhau tại O. Biết rằng tia Oy nằm giữa hai tia Ox và Oz.
a. Vẽ hình và kể tên các góc kề với
b. Cho = $40^{\circ}$ $\widehat{xOy'}$

6. ho hai góc kề bù và $\widehat{yOt}$, biết = $50^{\circ}$
a. TÍnh .
b. Trên cùng nửa mặt phẳng có bờ chứa tia Oy, Vẽ tia Oz sao cho = $80^{\circ}$. Chứng tỏ Oy là tia phân giác của $\widehat{xOz}$
c. Vẽ Oa là phân giác của . Tính $\widehat{aOt}$. Chứng tỏ $\widehat{aOy}$ là góc vuông.

Bài làm:

1. A =

2. a)

b)

3.
Vậy:

4. Trong 1 giờ, vòi thứ nhất chảy được bể; vời thứ hai chảy được $\frac{1}{8}$ bể. Lại có 1 giờ 15 phút = $\frac{5}{4}$ giờ vòi thứ nhất chảy được $\frac{5}{4}$.=$\frac{5}{24}$ (bể)
Phần còn lại là: 1- =$\frac{19}{24}$ (bể)
Vậy vòi thứ hai phải chảy hết = bể trong khoảng thời gian là:
: $\frac{1}{8}$ = $\frac{19}{3}$ (giờ); $\frac{19}{3}$ giờ = 6$\frac{1}{3}$ giờ = 6 giờ 20 phút.

5.

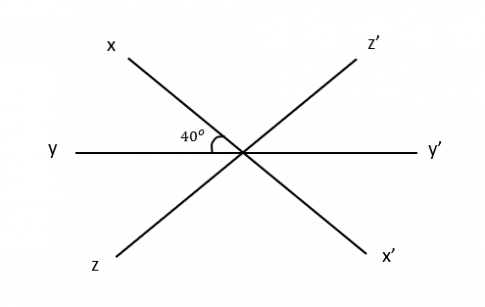
a) Các góc kề với là $\widehat{xOz'}$; $\widehat{yOz}$; $\widehat{xOy'}$; $\widehat{yOx'}$.
b) Vì Oy' và Oy là hai tia đối nhau nên và $\widehat{xOy'}$ là hai góc kề bù.
Ta có: + $\widehat{xOy'}$ = $180^{\circ}$
+ $\widehat{xOy'}$ = $180^{\circ}$
= $180^{\circ} - 40^{\circ} = 140^{\circ}$

6.

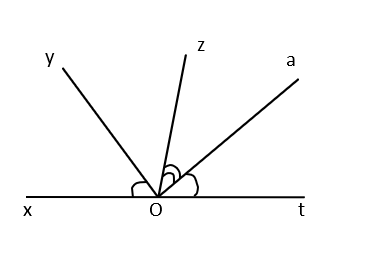
a) Vì và $\widehat{yOt}$ là hai góc kè bù nên
ta có: + $\widehat{yOt}$ = $180^{\circ}$
50^{\circ} + = $180^{\circ}$
= $180^{\circ} - 50^{\circ} = 130^{\circ}$
b) Trên cùng nửa mặt phẳng bờ chứa tia Oy mà < $\widehat{tOy}$ ($80^{\circ} < 130^{\circ}$) nên tia Oz nằm giữa hai tia Oy và Ot.
Ta có: + $\widehat{tOz}$ = $\widehat{yOt}$
+ $80^{\circ}$ = $130^{\circ}$
= $130^{\circ}$ - $80^{\circ}$ = $50^{\circ}$
Do đó = $\widehat{xOy}$ = $50^{\circ}$. Hiển nhiên tia Oy nằm giữa hai tia Ox và Oz.
Vậy Oy là tia phân giác của
c) Ta có Oa là tia phân giác của . Ta có $\widehat{tOa}$ = $\widehat{zOa}$ = $\frac{\widehat{tOz}}{2} = 40^{\circ}$.
Vì Oa và Oy cùng nằm trên nửa mặt phẳng bờ Ot mà nên tia Oa nằm giữa hai tia Oy và Ot.
Ta có: