Giải câu 1 trang 84 sách toán VNEN lớp 8 tập 2
D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNG
Câu 1: Trang 84 sách VNEN 8 tập 2
Cho tam giác ABC nhọn, đường cao BD, CE cắt nhau tại H.
a) Chứng minh rằng AD.AC = AE.AB và ![]() = $\widehat{ADE}$.
= $\widehat{ADE}$.
b) Chứng minh rằng ![]() HED và
HED và ![]() HBC đồng dạng.
HBC đồng dạng.
c) Chứng minh rằng BE.BA + CD.CA = ![]() .
.
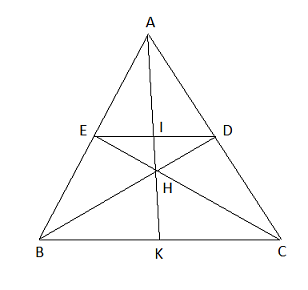
d) Nếu ![]() ABC đều hãy tính tỉ số diện tích
ABC đều hãy tính tỉ số diện tích ![]() HED và diện tích
HED và diện tích ![]() ABC.
ABC.
Bài làm:
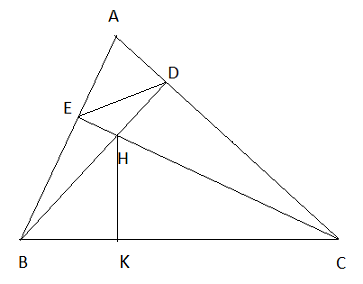
a) * ![]() ADB và
ADB và ![]() AEC có góc A chung, $\widehat{ADB}$ = $\widehat{AEC}$ nên
AEC có góc A chung, $\widehat{ADB}$ = $\widehat{AEC}$ nên ![]() ADB $\sim $
ADB $\sim $ ![]() AEC
AEC
![]() $\frac{AD}{AE}$ = $\frac{AB}{AC}$ $\Leftrightarrow $ AD.AC = AE.AB.
$\frac{AD}{AE}$ = $\frac{AB}{AC}$ $\Leftrightarrow $ AD.AC = AE.AB.
* ![]() ADE và
ADE và ![]() ABC có góc A chung, $\frac{AD}{AE}$ = $\frac{AB}{AC}$ nên
ABC có góc A chung, $\frac{AD}{AE}$ = $\frac{AB}{AC}$ nên ![]() ADE $\sim $
ADE $\sim $ ![]() ABC.
ABC.
![]() $\widehat{ABC}$ = $\widehat{ADE}$.
$\widehat{ABC}$ = $\widehat{ADE}$.
b)
Ta có: ![]() + $\widehat{ADE}$ = $90^{\circ}$
+ $\widehat{ADE}$ = $90^{\circ}$
![]() + $\widehat{ABC}$ = $90^{\circ}$
+ $\widehat{ABC}$ = $90^{\circ}$
Mặt khác ![]() = $\widehat{ABC}$ (theo câu a) $\Rightarrow $ $\widehat{HDE}$ = $\widehat{HCB}$ (1)
= $\widehat{ABC}$ (theo câu a) $\Rightarrow $ $\widehat{HDE}$ = $\widehat{HCB}$ (1)
Tương tự ta được ![]() = $\widehat{HBC}$ (2)
= $\widehat{HBC}$ (2)
Từ (1) và (2) suy ra ![]() HED $\sim $
HED $\sim $ ![]() HBC
HBC
c) Dựng HK vuông góc với BC
Ta có: ![]() BKH $\sim $
BKH $\sim $ ![]() BDC nên $\frac{BK}{BD}$ = $\frac{BH}{BC}$ $\Leftrightarrow $ BK.BC = BH.BD
BDC nên $\frac{BK}{BD}$ = $\frac{BH}{BC}$ $\Leftrightarrow $ BK.BC = BH.BD
![]() CKH $\sim $
CKH $\sim $ ![]() CEB nên $\frac{CK}{CE}$ = $\frac{CH}{BC}$ $\Leftrightarrow $ CK.BC = CH.CE
CEB nên $\frac{CK}{CE}$ = $\frac{CH}{BC}$ $\Leftrightarrow $ CK.BC = CH.CE
![]() BK.BC + CK.BC = BH.BD + CH.CE $\Leftrightarrow $ BC.(BK + CK) = BH.BD + CH.CE $\Leftrightarrow $ $BC^{2}$ = BH.BD + CH.CE
BK.BC + CK.BC = BH.BD + CH.CE $\Leftrightarrow $ BC.(BK + CK) = BH.BD + CH.CE $\Leftrightarrow $ $BC^{2}$ = BH.BD + CH.CE
Ta có: ![]() BEH $\sim $
BEH $\sim $ ![]() BDA nên: $\frac{BE}{BD}$ = $\frac{BH}{BA}$ $\Leftrightarrow $ BH.BD = BE.BA
BDA nên: $\frac{BE}{BD}$ = $\frac{BH}{BA}$ $\Leftrightarrow $ BH.BD = BE.BA
Tương tự ta được CH.CE = CD.CA
Suy ra ![]() = BE.BA + CD.CA.
= BE.BA + CD.CA.
d)
Xem thêm bài viết khác
- Giải toán VNEN 8 bài 1: Tỉ số của hai đoạn thẳng. Định lí Ta-lét trong tam giác
- Giải câu 3 trang 110 sách toán VNEN lớp 8 tập 2
- Giải câu 8 trang 93 sách toán VNEN lớp 8 tập 2
- Giải câu 4 trang 116 sách toán VNEN lớp 8 tập 2
- Giải câu 2 (E) trang 29 sách toán VNEN lớp 8 tập 2
- Giải câu 1 trang 59 sách toán VNEN lớp 8 tập 2
- Giải toán VNEN 8 bài 2: Phương trình bậc nhất một ẩn
- Giải câu 2 trang 113 sách toán VNEN lớp 8 tập 2
- Giải câu 2 trang 17 sách toán VNEN lớp 8 tập 2
- Giải câu 4 trang 41 sách toán VNEN lớp 8 tập 2
- Giải câu 2 trang 116 sách toán VNEN lớp 8 tập 2
- Giải câu 3 trang 21 sách toán VNEN lớp 8 tập 2











