Giải câu 2 đề 7 ôn thi toán lớp 9 lên 10
Bài 2: (2,0 điểm)
1. Cho 2 hàm số ![]() và $(d): y = -3x + 4$
và $(d): y = -3x + 4$
a. Vẽ 2 đồ thị trên cùng một mặt phẳng tọa độ Oxy
b. Tìm tọa độ giao điểm của 2 đồ thị trên bằng phép tính.
2. Cho phương trình ![]() .
.
Chứng minh rằng phương trình luôn có 2 nghiệm phân biệt với mọi m. Gọi 2 nghiệm của phương trình là ![]() , tìm tất cả giá trị của m sao cho $x_{1}^{2} + x_{1} - x_{2} = 5 - 2m$
, tìm tất cả giá trị của m sao cho $x_{1}^{2} + x_{1} - x_{2} = 5 - 2m$
Bài làm:
1. Cho 2 hàm số ![]() và $(d): y = -3x + 4$
và $(d): y = -3x + 4$
a. Xét hàm số: ![]()
Bảng giá trị
| x | -2 | -1 | 0 | 1 | 2 |
| y = 2x2 | 4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số ![]() là đường parabol nằm phía trên trục hoành, nhận trục Oy là trục đối xứng và nhận đỉnh O (0;0) làm điểm thấp nhất
là đường parabol nằm phía trên trục hoành, nhận trục Oy là trục đối xứng và nhận đỉnh O (0;0) làm điểm thấp nhất
Xét hàm số ![]()
Bảng giá trị
| x | 0 | 1 |
| y = -3x + 4 | 4 | 1 |
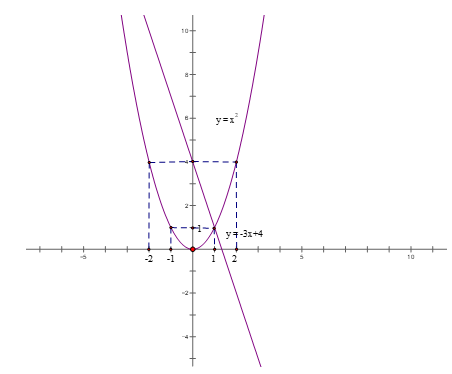
b. phương trình hoành độ giao điểm của (P) và (d) là
![]() ⇔ $x^{2} + 3x - 4 = 0$
⇔ $x^{2} + 3x - 4 = 0$
=> phương trình có nghiệm x = 1 và x = - 4 ( do phương trình có dạng a + b + c =0)
Với x = 1 thì y = 1
Với x = - 4 thì y = 16
Vậy tọa độ giao điểm của (P) và (d) là (1; 1 ) và (-4; 16)
2. ![]() .
.
![]()
Vậy phương trình luôn có 2 nghiệm phân biệt với mọi m
Theo định lí Vi- ét ta có:
![]()
⇔ ![]()
⇔![]()
⇔ ![]()
![]()
Với ![]() thay vào phương trình ban đầu tìm được $m=\frac{3}{4}$
thay vào phương trình ban đầu tìm được $m=\frac{3}{4}$
Với ![]() thay vào phương trình ban đầu, tìm được m $m=\frac{-3}{4}$
thay vào phương trình ban đầu, tìm được m $m=\frac{-3}{4}$
Vậy với ![]() thì phương trình có 2 nghiệm thỏa mãn yêu cầu đề bài.
thì phương trình có 2 nghiệm thỏa mãn yêu cầu đề bài.
Xem thêm bài viết khác
- Đề thi thử Toán vào lớp 10 THPT chuyên tỉnh Thái Nguyên 2022 Đề thi thử Toán vào 10 chuyên Thái Nguyên (Đề đại trà)
- Đề thi thử Toán vào 10 trường THCS Trần Mai Ninh năm 2022 Đề thi thử Toán vào lớp 10 năm 2022
- Giải câu 5 đề 20 ôn thi toán lớp 9 lên 10
- Đáp án đề thi vào lớp 10 môn Toán Sơn La năm 2022 Đề thi môn Toán vào lớp 10 tỉnh Sơn La năm 2022
- Giải câu 4 đề 9 ôn thi toán lớp 9 lên 10
- Đề thi vào 10 chuyên Toán trường THPT Chuyên KHXH&NV năm 2022 Đề thi vào 10 chuyên Toán năm 2022
- Đề thi thử vào lớp 10 môn Toán trường THPT chuyên Hà Nội - Amsterdam năm 2022 Đề thi thử vào lớp 10 môn Toán 2022
- Giải câu 1 đề 11 ôn thi toán lớp 9 lên 10
- Đề thi vào lớp 10 môn Toán trường THPT chuyên Lê Hồng Phong, Nam Định năm 2022 Đề thi vào lớp 10 môn Toán 2022
- Đề thi vào lớp 10 chuyên Toán trường THPT chuyên Lê Hồng Phong, Nam Định năm 2022 Đề thi vào lớp 10 môn Toán 2022
- Đề thi thử vào 10 môn Toán trường THCS Ái Mộ năm 2022 Đề thi thử vào lớp 10 môn Toán 2022
- Lời giải bài 1 chuyên đề Bài toán Dựng hình











