Giải câu 3 trang 83 sách toán VNEN lớp 8 tập 2
Câu 3: Trang 83 sách VNEN 8 tập 2
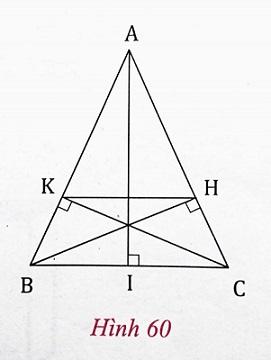
Cho tam giác cân ABC (AB = AC), vẽ các đường cao BH, CK (h,60). Chứng minh:
a) Tìm các cặp tam giác đồng dạng có trong hình và giải thích.
b) Cho biết BC = a, AB = AC = b. Tính độ dài đoạn thẳng HK.
Hướng dẫn câu b):
- Vẽ thêm đường cao AI, xét hai tam giác đồng dạng IAC và HBC rồi tính CH.
- Tiếp theo, xét hai tam giác đồng dạng AKH và ABC rồi tính HK.
Bài làm:
a) * ![]() KCB và
KCB và ![]() HBC có $\widehat{ABC}$ = $\widehat{ACB}$ (do tam giác ABC cân), $\widehat{BKC}$ = $\widehat{BHC}$, BC chung nên
HBC có $\widehat{ABC}$ = $\widehat{ACB}$ (do tam giác ABC cân), $\widehat{BKC}$ = $\widehat{BHC}$, BC chung nên ![]() KCB =
KCB = ![]() HBC
HBC
![]() BK = HC
BK = HC ![]() AK = AH
AK = AH
* ![]() AKH và
AKH và ![]() ABC có góc A chung, $\frac{AK}{AB}$ = $\frac{AH}{AC}$ nên
ABC có góc A chung, $\frac{AK}{AB}$ = $\frac{AH}{AC}$ nên ![]() AKH $\sim $
AKH $\sim $ ![]() ABC
ABC
* Gọi giao điểm của BH và CK là O
Vì ![]() = $\frac{AH}{AC}$ nên KH // BC
= $\frac{AH}{AC}$ nên KH // BC
![]() OKH và
OKH và ![]() OCB có $\widehat{OKH}$ = $\widehat{OCB}$, $\widehat{OHK}$ = $\widehat{OBC}$ (so le trong) nên
OCB có $\widehat{OKH}$ = $\widehat{OCB}$, $\widehat{OHK}$ = $\widehat{OBC}$ (so le trong) nên ![]() OKH $\sim $
OKH $\sim $ ![]() OCB.
OCB.
b) Vẽ đường cao AI
![]() IAC và
IAC và ![]() HBC có góc C chung, $\widehat{AIC}$ = $\widehat{BHC}$ nên
HBC có góc C chung, $\widehat{AIC}$ = $\widehat{BHC}$ nên ![]() IAC $\sim $
IAC $\sim $ ![]() HBC
HBC
![]() $\frac{HC}{IC}$ = $\frac{BC}{AC}$ $\Leftrightarrow $ $\frac{HC}{\frac{a}{2}}$ = $\frac{a}{b}$ $\Leftrightarrow $ HC = $\frac{a^{2}}{2b}$
$\frac{HC}{IC}$ = $\frac{BC}{AC}$ $\Leftrightarrow $ $\frac{HC}{\frac{a}{2}}$ = $\frac{a}{b}$ $\Leftrightarrow $ HC = $\frac{a^{2}}{2b}$ ![]() AH = AC - HC = b - $\frac{a^{2}}{2b}$ = $\frac{2b^{2}- a^{2}}{2b}$.
AH = AC - HC = b - $\frac{a^{2}}{2b}$ = $\frac{2b^{2}- a^{2}}{2b}$.
Theo câu a) ![]() AKH $\sim $
AKH $\sim $ ![]() ABC nên
ABC nên
![]() = $\frac{AH}{AC}$ $\Rightarrow $ HK = $\frac{AH.BC}{AC}$ = $\frac{\frac{2b^{2}- a^{2}}{2b}.a}{b}$ = $\frac{(2b^{2}- a^{2}).a}{2b^{2}}$ = a - $\frac{a^{3}}{2b^{2}}$
= $\frac{AH}{AC}$ $\Rightarrow $ HK = $\frac{AH.BC}{AC}$ = $\frac{\frac{2b^{2}- a^{2}}{2b}.a}{b}$ = $\frac{(2b^{2}- a^{2}).a}{2b^{2}}$ = a - $\frac{a^{3}}{2b^{2}}$
Xem thêm bài viết khác
- Giải câu 3 trang 53 sách toán VNEN lớp 8 tập 2
- Giải câu 1 trang 83 sách toán VNEN lớp 8 tập 2
- Giải câu 1 trang 106 sách toán VNEN lớp 8 tập 2
- Giải câu 3 trang 24 sách toán VNEN lớp 8 tập 2
- Giải câu 4 trang 92 sách toán VNEN lớp 8 tập 2
- Giải câu 3 trang 100 sách toán VNEN lớp 8 tập 2
- Giải câu 2 trang 46 sách toán VNEN lớp 8 tập 2
- Giải câu 2 trang 68 sách toán VNEN lớp 8 tập 2
- Giải câu 6 trang 92 sách toán VNEN lớp 8 tập 2
- Giải câu 6 trang 41 sách toán VNEN lớp 8 tập 2
- Giải câu 1 trang 84 sách toán VNEN lớp 8 tập 2
- Giải toán VNEN 8 bài 3: Luyện tập chung











