Giải câu 3 trang 98 toán VNEN 8 tập 1

Câu 3: Trang 98 toán VNEN 8 tập 1

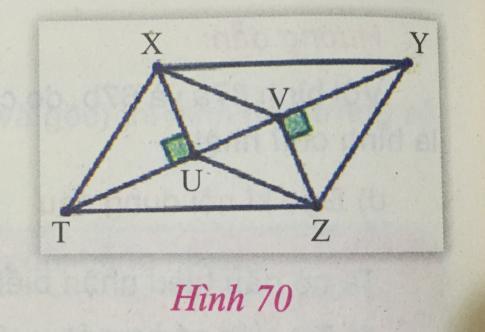
Cho hình bình hành XYZT. Gọi U, V tương ứng là hình chiếu vuông góc của X và Z trên YT (hình 70). Chứng minh rằng XYZT là hình bình hành.

Bài làm:

Có XU và VZ cùng vuông góc với YT (gt) nên XU // VZ. (1)

Xét XTU vuông tại U và ZYV vuông tại V, có:

XT = ZY (gt)

= $\widehat{ZYV}$ (so le trong)

$\Delta$XTU = $\Delta$ZYV (cạnh huyền – góc nhọn)

XU = VZ. (2)

Từ (1) và (2) XVZU là hình bình hành.