Giải câu 5 trang 137 toán VNEN 8 tập 1

Câu 5: Trang 137 toán VNEN 8 tập 1

Cho hình thang cân ABCD, có đáy nhỏ AB = 6cm, đáy lớn CD = 12cm và cạnh bên AD = 5cm (hình 136). Gọi M, N, E, G tương ứng là trung điểm của các cạnh AD, BC, AB, CD.

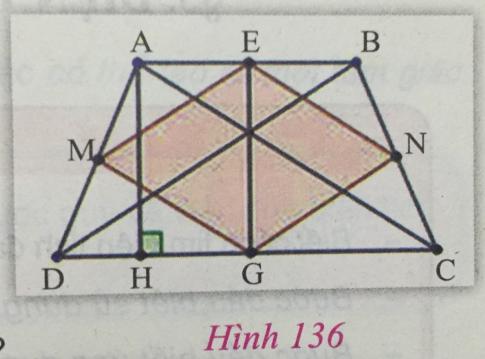
a) Chứng minh rằng MENG là hình thoi.

b) Diện tích hình thoi MENG bằng bao nhiêu cm?

Bài làm:

a) Xét ACD, có: M là trung điểm AD và G là trung điểm DC

MG là đường trung bình của $\mathrm{\Delta }$ACD MG = $\frac{1}{2}$AC. (1)

Xét ABC, có: E là trung điểm AB và N là trung điểm BC

EN là đường trung bình của $\mathrm{\Delta }$ABC EN = $\frac{1}{2}$AC. (2)

Từ (1) và (2) MG = EN = $\frac{1}{2}$AC. (*)

Chứng minh tương tự, ta có: EM = GN = BD. (**)

Mà ABCD là hình thang cân nên AC = BD.(***)

Từ (*), (**) và (***) MENG là hình thoi (đpcm).

b) S = $\frac{1}{2}$EG.MN = $\frac{1}{2}$AH. $\frac{1}{2}$.(AB + CD) = $\frac{1}{2}$.4. $\frac{1}{2}$.(6 + 12) = 18 (cm${}^2$).