Giải câu 2 trang 126 toán VNEN 8 tập 1

D. Hoạt động vận dụng

Câu 2: Trang 126 toán VNEN 8 tập 1

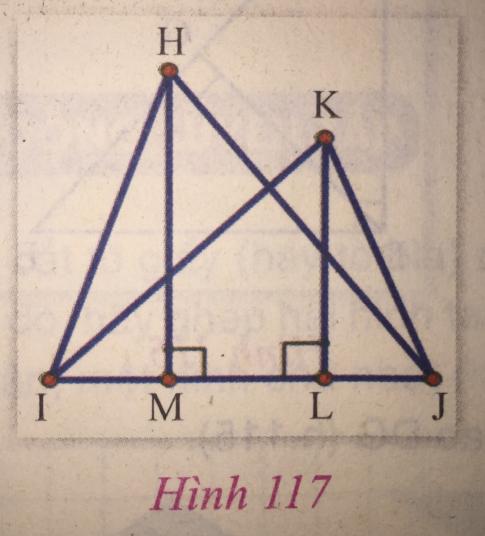
a) Cho tam giác HIJ có đường cao HM, tam giác KIJ có đường cao KL (hình 117). Chứng minh rằng: _{KIJ}}$ = $\frac{HM}{KL}$.

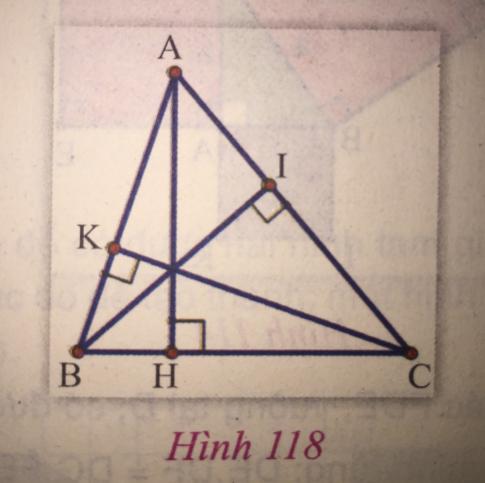
b) Cho tam giác ABC với các đường cao AH, BI, CK (hình 118). Chứng minh rằng: AH.BC = BI.CA = CK.AB.

Bài làm:

a) Ta có: S = $\frac{HM.IJ}{2}$ và S$_{KIJ}$ = $\frac{KL.IJ}{2}$.

Như vậy: _{KIJ}}$ = $\frac{\frac{HM.IJ}{2}}{\frac{KL.IJ}{2}}$ = $\frac{HM.IJ}{2}$ . $\frac{2}{KL.IJ}$ = $\frac{HM}{KL}$ (đpcm).

b) Vì AH, BI, CK đều là đường cao của tam giác ABC nên ta có:

S = $\frac{AH.BC}{2}$ = $\frac{BI.AC}{2}$ = $\frac{CK.AB }{2}$

AH.BC = BI.CA = CK.AB (đpcm).