Lời giải bài 1 chuyên đề Bài toán Dựng hình

Bài 1: Dựng tam giác ABC ,biết cạnh BC = a ,trung tuyến AM = m (a và m là những độ dài cho trước ) và góc giữa AM và đường cao AH.

Bài làm:

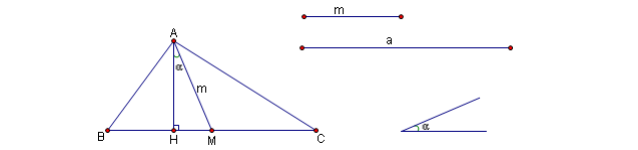
Phân tích :

Giả sử bài toán đã giải xong,và ta đã dựng được tam giác ABC thoả mãn yêu cầu của đề toán .Phân tích hình đó theo hướng phát hiện một bộ phận của hình hội đủ các điều kiện để dựng được một cách chính xác:

• Đó là tam giác vuông AHM có cạnh huyền AM = m
• cho trước.

=> Tam giác đó hoàn toàn xác định nên dựng được. Sau khi dựng xong tam giác vuông AHM ,ta hoàn tất hình phải dựng .

Cách dựng hình :

• Dựng đoạn thẳng AM có độ dài m cho trước ( phép dựng cơ bản 1 ).
• Dựng cho trước ( phép dựng cơ bản 2 ).
• Từ M kẻ tại H ( phép dựng cơ bản 5 ).
• Bây giờ chỉ còn dựng hai đỉnh B,C .Cạnh BC nằm trên đường thẳng MH ,nên trên đường thẳng MH ,ta lấy ở hai phía khác nhau đối với điểm M hai điểmB và C sao cho MB = MC = ( phép dựng cơ bản 3 và 1 ).

Chứng minh :

Rõ ràng tam giác trên đây thoả mãn đầy đủ các yêu cầu của đề toán :

• cạnh BC = a cho trước.
• trung tuyến AM = m cho trước .
• cho trước .

Biện luận :

Xét từng bước dựng hình , bước nào cũng được thực hiện rõ ràng, mạch lạc.Duy chỉ có góc cho trước và yêu cầu đề ra là $\widehat{MAH}$ của tam giác vuông AMH phải bằng ,thì rõ ràng phải là góc nhọn .Vậy với điều kiện này thì bài toán bao giờ cũng giải được và có một nghiệm hình .