Lời giải bài số 34, 49, 50- đề thi thử THPT Quốc gia môn toán Sở GD và ĐT Đà Nẵng

1 Đánh giá

Bài làm:

Câu 34: Trong không gian hệ trục tọa độ Oxyz, cho ba điểm A(2,3,-4), B(4,1,2), C(-3,2,-7). Gọi N là trung điểm của AB. Biết rằng tập hợp tất cả các điểm M thỏa mãn điều kiện $|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+3\overrightarrow{MN}|=12$ là một mặt cầu. Tìm tâm I và bán kính R của mặt cầu đó.

A. I(4,4,-4) và R=12.

B. I(2,2,-2) và R=12.

C. I(4,4,-4) và R=2.

D. I(2,2,-2) và R=-2.

Giải: Đáp án D.

Ta có $\overrightarrow{AB}=(2,-2,6),\overrightarrow{AC}=(-5,-1,-3)$ , vì $\overrightarrow{AB}\neq k \overrightarrow{AC}\Rightarrow $ A, B, C không thẳng hàng.

Gọi G là trọng tâm của tam giác ABC thì G(1,2,-3). Gọi M(x,y,z); N(3,2,-1)/

Vì vậy $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$ $\Rightarrow |\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+3\overrightarrow{MN}|=|3\overrightarrow{MG}+3\overrightarrow{MN}|=3|2\overrightarrow{MN}+\overrightarrow{NG}|=12$

$\Rightarrow |2\overrightarrow{MN}+\overrightarrow{NG}|=4$ .

Ta có $2\overrightarrow{MN}=(6-2x,4-2y,-2-2z), \overrightarrow{NG}=(-2,0,-2) \Rightarrow 2\overrightarrow{MN}+\overrightarrow{NG}=2(2-x,2-y,-2-z)$ .

$\Rightarrow 4[(x-2)^{2}+(y-2)^{2}+(z+2)^{2}]=16 \Rightarrow (x-2)^{2}+(y-2)^{2}+(z+2)^{2}=4$

Vậy $I(2,2,-2),R=2$ .

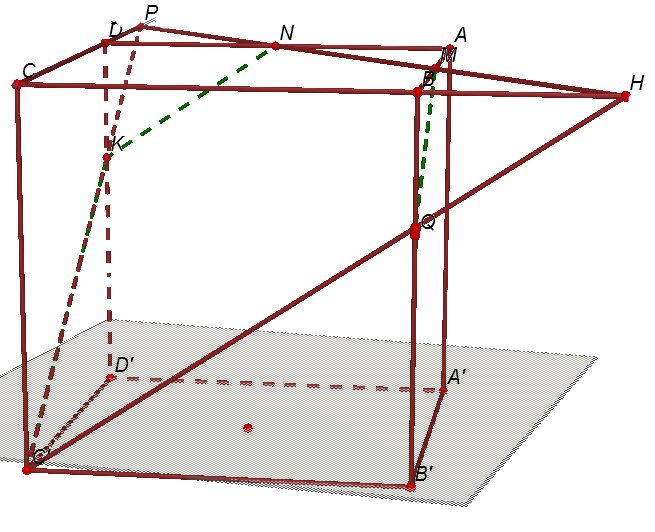Câu 49: Cho khối hình lập phương ABCD.A'B'C'D'. Gọi M, N lần lượt là trung điểm của AB và AD, mặt phẳng (C'MN) chia khối lập phương thành 2 khối đa diện, đặt $V_{1}$ là thể tích khối đa diện nhỏ và $V_{2}$ là thể tích khối đa diện lớn. Tính $\frac{V_{1}}{V_{2}}$.

A. $\frac{V_{1}}{V_{2}}=\frac{1}{3}$ .

B. $\frac{V_{1}}{V_{2}}=\frac{13}{23}$ .

C. $\frac{V_{1}}{V_{2}}=\frac{1}{2}$ .

D. $\frac{V_{1}}{V_{2}}=\frac{25}{47}$ .

Giải: Đáp án D.

Kéo dài MN cắt BC tại H, nối HC' cắt BB' tại Q, ta có $\frac{HB}{HC}=\frac{QN}{CC'} \Rightarrow QB=\frac{a}{3}$ .

Tương tự: Kéo dài MN cắt DC tại P, nối PC' cắt DD' tại K $\Rightarrow DK=\frac{a}{3}$ .

Thể tích đa diện nhỏ $C'KNMQBCD=V_{1}$

$V_{1}=V_{C'NDCBM}+V_{C'MQB}+V_{C'KND}=V_{C'NDCBM}+2V_{C'MQB}$

$V_{C'NDCBM}=\frac{1}{3} a(a^{2}-\frac{1}{2}.\frac{a}{2}.\frac{a}{2})=\frac{7a^{3}}{24}; V_{C'MQB}=\frac{1}{3}a.\frac{1}{2}.\frac{a}{3}.\frac{a}{2}=\frac{a^{3}}{36}$

$\Rightarrow V_{1}=\frac{25a^{3}}{72}\Rightarrow V_{2}=a^{3}-\frac{25a^{3}}{72}=\frac{47a^{3}}{72}$ .

Câu 50: Cho $z_{1}, z_{2}$ là hai số phức thỏa mãn $|z_{1}|=|z_{2}|=1$ và $|z_{1}-z_{2}|=\sqrt{2}$. Tính $P=|\frac{1}{2}z_{1}+\frac{1}{2}z_{2}|.$

A. $P=\frac{\sqrt{2}}{2}$ .

B. $P=\frac{1}{2}$ .

C. $P=\frac{\sqrt{2}}{4}$ .

D. $P=\frac{\sqrt{3}}{3}$ .

Giải: Đáp án A.

Gọi $z_{1}=a+bi, z_{2}=c+di$ ta có

$\left\{\begin{matrix} a^{2}+b^{2}=c^{2}+d^{2}=1\\(a-c)^{2}+(b-d)^{2}=2 \\ p^{2}=\frac{1}{4}[(a+c)^{2}+(b+d)^{2}]\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a^{2}+b^{2}=c^{2}+d^{2}=1\\2(ac+bd)=0 \\ p^{2}=\frac{1}{4}=\frac{1}{2}\end{matrix}\right.\Rightarrow P=\frac{\sqrt{2}}{2}$ .

3 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Tuyển tập đề thi THPT quốc gia môn Toán