Lời giải bài số 6, 38, 42 Đề thi thử THPT quốc gia môn toán năm 2017- Đề tham khảo số 12
Bài làm:
Câu 6: Tìm các giá trị của tham số m để giá trị nhỏ nhất của hàm số ![]() trên [0,1] bằng -2.
trên [0,1] bằng -2.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Giải: Đáp án D.
Ta có ![]() nên hàm số đã cho đồng biến trên [0,1].
nên hàm số đã cho đồng biến trên [0,1].
Do đó: ![]() .
.
Câu 38: Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh ạ. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc AB sao cho HB=2HA. Cạnh SC tạo với mặt phẳng đáy (ABCD) một góc bằng ![]() . Khoảng cách từ trung điểm K của HC đến mặt phẳng (SCD) là:
. Khoảng cách từ trung điểm K của HC đến mặt phẳng (SCD) là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
 Giải: Đáp án D.
Giải: Đáp án D.
Xét H là hình chiếu vuông góc của S lên (ABCD) nên ![]() .
.
Xét tam giác BHC vuông tại B có ![]() .
.
Xét tam giác SHC vuông tại H, ![]() nên có $SH=HC. \tan 60^{0}$.
nên có $SH=HC. \tan 60^{0}$.
Gọi M là điểm trên cạnh CD thỏa mãn ![]() , suy ra $(SHM) \perp (SCD)$ theo giao tuyến SM.
, suy ra $(SHM) \perp (SCD)$ theo giao tuyến SM.
Dựng ![]() tại I suy ra $HI=d(H, (SCD))$. Xét tam giác SHM vuông tại H có đường cao HI nên
tại I suy ra $HI=d(H, (SCD))$. Xét tam giác SHM vuông tại H có đường cao HI nên
 .
.
Vì K là trung điểm của HC nên có ![]() .
.
Câu 42: Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
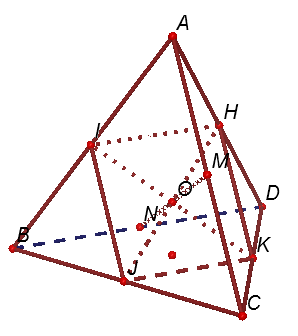 Giải: Đáp án B.
Giải: Đáp án B.
Gọi I, J, K, H, M, N lần lượt là trung điểm AB, BC, CD, DA, AC, BD. Théo tính chất hình bình hành ta chứng minh được IK, JH, MN cắt nhau tại trung điểm mỗi đường, gọi là giao điểm O. Vì tứ diện ABCD đều nên
![]() .
.
Suy ra O là tâm mặt cầu tiếp xúc với các cạnh của tứ diện ABCD.
Xét hình vuông IJKH cạnh ![]()
![]() .
.
Chú ý: Học sinh thường mắc sai lầm khi tiếp lầm tưởng tiếp xúc với các cạnh là khối cầu nội tiếp mặt cầu.
Xem thêm bài viết khác
- Thi THPTQG 2020: Đề thi và đáp án môn Toán mã đề 112
- Đáp án đề thi thử THPT quốc gia môn toán năm 2017- đề tham khảo số 11
- Thi THPTQG 2020: Đề thi và đáp án môn Toán mã đề 115
- Lời giải bài số 40, 41, 42, 46 Đề thi thử THPT quốc gia môn toán năm 2017 của trường THPT chuyên Quốc học Huế lần 3
- Thi THPTQG 2019: Đề thi và đáp án môn Toán mã đề 112
- Đề và đáp án môn Toán mã đề 113 thi THPT quốc gia năm 2017 đáp án của bộ GD-ĐT
- Thi THPTQG 2020: Đề thi và đáp án môn Toán mã đề 103
- Đáp án Đề thi thử THPT quốc gia môn toán năm 2017 của Sở GD- ĐT Đà Nẵng
- Thi THPTQG 2019: Đề thi và đáp án môn Toán mã đề 122
- Đề thi thử THPT quốc gia môn toán năm 2017 của Sở GD và ĐT Đà Nẵng
- Đề thi khảo sát chất lượng môn toán năm 2017- Sở giáo dục đào tạo Thanh Hóa
- Thi THPTQG 2020: Đề thi và đáp án môn Toán mã đề 118











