Đáp án câu 4 đề 10 kiểm tra học kì 2 Toán 9

Câu 4(3 điểm): Cho tam giác ABC vuông tại A, M là trung điểm của cạnh AC. Vẽ đường tròn đường kính MC cắt cạnh BC tại N (N C). Đường thẳng BM cắt đường tròn đường kính MC tại D (D M). Chứng minh:

a, Tứ giác BADC nội tiếp được trong một đường tròn. Xác định tâm O của đường tròn đó.

b, CM.CA = CN.CB

c, = ON.OC

Bài làm:

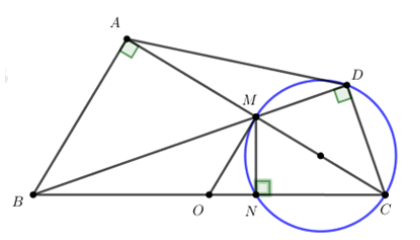
a, Ta có: D thuộc đường tròn đường kính MC nên hay $\widehat{BDC} = 90^{\circ}$

Nên D thuộc đường tròn đường kính BC (1)

Có: nên A thuộc đường tròn đường kính BC (2)

Từ (1) và (2) Hay tứ giác BADC nội tiếp đường tròn đường kính BC.

Gọi O là trung điểm của BC, khi đó ta có tâm O của đường tròn chính là trung điểm của BC và bán kính chính bằng nửa độ dài BC.

b, Xét và $\Delta CBA$ ta có:

+, chung

+,

(g.g)

c, Ta có: O là trung điểm của BC (cm câu a)

M là trung điểm của AC (gt)

OM là đường trung bình của tam giác ABC

Khi đó ta có: OM // AB. Mà AB AC

hay $OM \perp MC$

Xét vuông có MN là đường cao

(đpcm)