Giải câu 47 Bài 6: Cung chứa góc sgk Toán 9 tập 2 Trang 86

Câu 47: Trang 86 - SGK Toán 9 tập 2

Gọi cung chứa góc ở bài tập 46 là cung AmB. Lấy điểm $M_1$ nằm bên trong và điểm $M_2$ nằm bên ngoài đường tròn chứa cung này sao cho $M_1$, $M_2$ và cung AmB nằm cùng một phía đối với đường thẳng AB. Chứng minh rằng:

a)

b)

Bài làm:

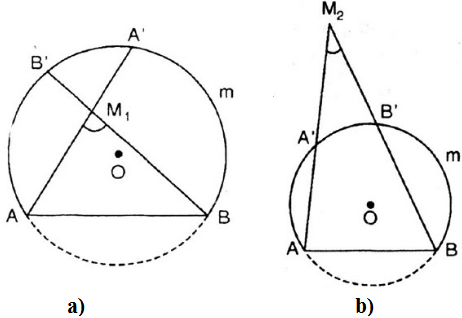
a) Điểm nằm bên trong cung chứa góc ${55}^{\circ }$.

Gọi lần lượt là giao điểm của $A{M}_1$, $B{M}_1$ với cung tròn AmB.

Vì là góc có đỉnh nằm trong đường tròn nên:

= $\frac{1}{2}$ (sđ cung AB + sđ cung A'B') = $\frac{1}{2}$ sđ cung AB +$\frac{1}{2}$ sđ cung A'B' = ${55}^{\circ }$ + $a$ ($a>0$)

=>

b) Điểm nằm bên trong cung chứa góc ${55}^{\circ }$.

Gọi lần lượt là giao điểm của $A{M}_2$, $B{M}_2$ với cung tròn AmB.

Vì là góc có đỉnh nằm ngoài đường tròn nên:

= $\frac{1}{2}$ (sđ cung AB - sđ cung A'B') = $\frac{1}{2}$ sđ cung AB - $\frac{1}{2}$ sđ cung A'B' = ${55}^{\circ }$ - $a$ ($a>0$)

=>