Đáp án câu 4 đề 3 kiểm tra học kì 2 Toán 9

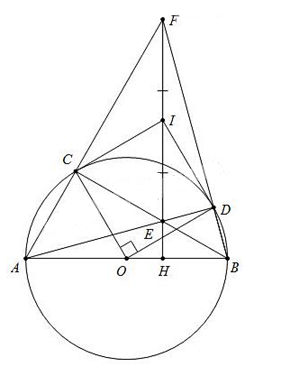
Câu 4(3,5 điểm): Cho nửa đường tròn (O) đường kính AB = 2R; C là điểm bất kì nằm trên đường tròn sao cho C khác A và AC < CB. Điểm D thuộc cung nhỏ BC sao cho . Gọi E là giao điểm của AD và BC, F là giao điểm của AC và BD.

a, Chứng minh CEDF là tứ giác nội tiếp

b, Chứng minh FC.FA = FD.FB

c, Gọi I là trung điểm của EF. Chứng minh IC là tiếp tuyến của (O)

d, Hỏi khi C thay đổi thỏa mãn điều kiện bài toán, E thuộc đường tròn cố định nào?

Bài làm:

a, Ta có:

Tứ giác CEDF có:

tứ giác CEDF là tứ giác nội tiếp.

b, Xét và $\mathrm{\Delta }FDA$ có $\widehat{FCB}=\widehat{FDA}={90}^{\circ }$ và chung $\widehat{CFB}$

(g.g)

FC.FA = FD.FB

Vậy FC.FA = FD.FB

c, Xét cân tại O nên $\widehat{ICF}=\widehat{IFC}$

cân tại I nên $\widehat{OAC}=\widehat{OCA}$

Do đó: vì $\mathrm{\Delta }HAF$ vuông tại H(do E là trực tâm $\mathrm{\Delta }FAB$)

Mà IC tiếp xúc với (O)

d, Gọi T là điểm chính giữa của cung AB không chứa C (T cố định)

IETO là hình bình hành (vì IE song song và bằng OT)

(vì ICOD là hình vuông cạnh E)

Vậy )