Giải Câu 37 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn sgk Toán 9 tập 2 Trang 82

Câu 37: Trang 82 – SGK Toán 9 tập 2

Cho đường tròn (O) và hai dây AB, AC bằng nhau. Trên cung nhỏ AC lấy một điểm M. Gọi S là giao điểm của AM và BC. Chứng minh = $\widehat{MCA}$

Bài làm:

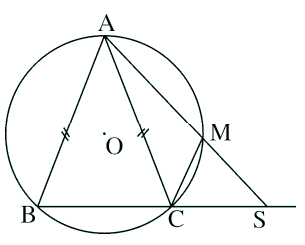
Ta có: là góc có đỉnh nằm ngoài đường tròn (O) => = $\frac{1}{2}$ (sđ cung AB - sđ cung MC)

Theo giả thiết: dây cung AB = dây cung AC => sđ cung AB = sđ cung AC

=> sđ cung AB - sđ cung MC = sđ cung AC - sđ cung MC = sđ cung AM (1)

Mặt khác: là góc nội tiếp chắn cung AM của (O) => $\widehat {ASC}$ = $\frac{1}{2}$ sđ cung AM (2)

Từ (1) (2) => = ( = $\frac{1}{2}$ sđ cung AM ) (đpcm)