Đáp án câu 4 đề 6 kiểm tra học kì 2 Toán 9

Câu 4(3,5 điểm): Cho tam giác ABC nhọn, nội tiếp đường tròn (O). Ba đường cao AD, BE, CF của tam giác ABC cùng đi qua trực tâm H.

a, Chứng minh: Tứ giác BFEC nội tiếp.

b, Kẻ đường kính AK của đường tròn (O).

Chứng minh: tam giác ABD đồng dạng với tam giác AKC và AB.AC = 2AD.R.

c, Gọi M là hình chiếu vuông góc của C trên AK. Chứng minh: MD song song với BK.

d, Giả sử BC là dây cố định của đường tròn (O) còn A di động trên cung lớn BC. Tìm vị trí của điểm A để diện tích tam giác AEH lớn nhất.

Bài làm:

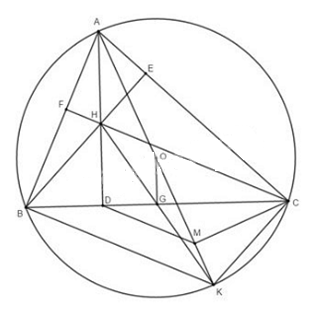
a, BE, CF là 2 đường cao của ABC $\Rightarrow \widehat{BEC} = \widehat{BFC} = 90^{\circ}$

Xét tứ giác BFEC có góc

Hai góc này cùng nhìn cạnh BC 1 góc nên tứ giác này nội tiếp.

b, Ta có:

(2 góc nội tiếp chắn cung AC của (O))

AK là đường kính của (O);

Xét và $\Delta AKC$ có $\widehat{ABD} = \widehat{AKC}$ và $\widehat{ADB} = \widehat{ACK}$

(g.g)

c, Tứ giác ADMC nội tiếp do có

Xét (O) có: (2 góc nội tiếp cùng chắn cung CK)

MD // BK

d, Ta có:

Mà có OG là đường trung bình $\Rightarrow AH = 2OG \Rightarrow S_{\Delta AEH} \leq OG^{2}$

O và G cố định lên . Dấu "=" xảy ra khi $AE = EH \Rightarrow \widehat{HAE} = 45^{\circ} \Rightarrow \widehat{ACB} = 45^{\circ}$