Đáp án câu 4 đề 9 kiểm tra học kì 2 Toán 9

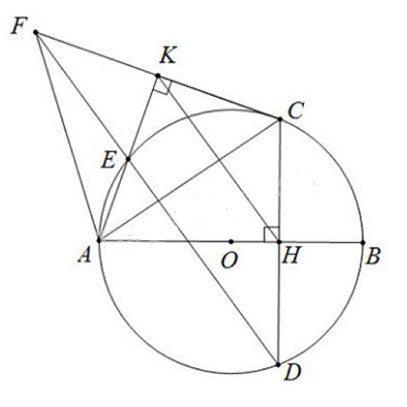
Câu 4(3 điểm): Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E bất kỳ (E khác A và C). Kẻ CK vuông góc với AE tại K. Đường thẳng DE cắt CK tại F.

a) Chứng minh tứ giác AHCK là tứ giác nội tiếp.

b) Chứng minh KH song song với ED và tam giác ACF là tam giác cân.

c) Tìm vị trí của điểm E để diện tích tam giác ADF lớn nhất.

Bài làm:

a, Vì CK AK nên $\widehat{AKC} = 90^{\circ}$

CH AB tại H nên $\widehat{AHC} = 90^{\circ}$

Xét tứ giác AHCK có: nên AHCK là tứ giác nội tiếp

b, Tứ giác AHCK nội tiếp (góc nội tiếp chắn cung CK)

Lại có ADCE nội tiếp (góc nội tiếp chắn cung CE)

HK // DE.

Do HK// DF, mà H là trung điểm CD (Được suy ra từ quan hệ vuông góc của đường kính AB với dây CD tại H ).

HK là đường trung bình của $\Delta CDF$

K là trung điểm FC.

có AK là đường cao đồng thời cũng là trung tuyến nên cân tại K .

c, cân tại A nên AF = AC.

Dễ thấy cân tại A nên AC = AD từ

AF = AD $\Rightarrow \Delta AFD$ cân tại A, hạ DI $\perp $ AF.

Ta có:

do AC không đổi nên lớn nhất khi và chỉ khi DI lớn nhất.

Trong vuông ta có:

hay $S_{\Delta AFD} \leq \frac{AC^{2}}{2}$. Dấu "=" xảy ra khi I $\equiv$ A khi đó $\widehat{DAF} = 90^{\circ} \Rightarrow \Delta ADF$ vuông cân tại A $\Rightarrow \widehat{EBA} = \widehat{EDA} = 45^{\circ}$ hay E là điểm chính giữa cung AB.