Đáp án câu 4 đề 5 kiểm tra học kì 2 Toán 9

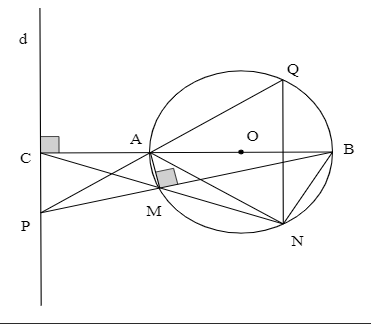
Câu 4(3,5 điểm): Cho đường tròn (O;R), đường kính AB. Trên tia đối của tia AB lấy điểm C (AC > R). Qua C kẻ đường thẳng d vuông góc với CA. Lấy điểm M trên đường tròn (O) sao cho AM = . Tia BM cắt đường thẳng d tại điểm P. Tia CM cắt đường tròn (O) tại điểm thứ hai là N, tia PA cắt đường tròn (O) tại điểm thứ hai là Q.

a, Chứng minh tứgiác ACPM là tứ giác nội tiếp

b, Chứng minh NQ // PC

c, 1,Tính thể tích của hình tạo thành khi quay tam giác MAB một vòng quanh AM theo R.

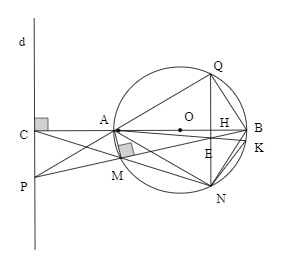
2,Gọi H là giao điểm của QN và AB. Gọi E là giao điểm của MB và QN, tia AE cắt đường tròn (O) tại điểm thứ hai là K. Chứng minh AE.AK + BE.BM = 4.

d, Chứng minh rằng ba điểm B, N và tâm đường tròn ngoại tiếp tam giác NEK thẳng hàng

Bài làm:

a, a, Ta có:

là góc nội tiếp chắn nửa đường tròn (O) $\Rightarrow \widehat{AMB} = 90^{\circ} \Rightarrow \widehat{AMP} = 90^{\circ}$

Xét tứ giác AMCP có:

tứ giác ACPM nội tiếp.

b, Tứ giác ACPM nội tiếp (1)( cùng chắn cung AC)

Mà (2)( do tứ giác AMNQ nội tiếp (O))

Từ (1) và (2)

$\Rightarrow CP // QN.

c,

1, vuông tại M $\Rightarrow AM^{2} + BM^{2} = AB^{2}$

Khi quay tam giác vuông AMB một vòng quanh cạnh AM ta được hình nón với đường cao h = AM = , bán kính của đường tròn đáy là r = BM = $\frac{\sqrt{15}}{2}R$. Thể tích của hình nón là:

V = (đvtt)

2, Có ; CP // QN $\Rightarrow $QN \perp AB$

Gọi H là giao điểm của AB và QN.

∆AEH ∆ABK (g.g) $\Rightarrow \frac{AE}{AB} = \frac{AH}{AK} \Rightarrow AE.AK = AB.AH$ (1)

∆BEH ∆BAM (g.g) $\Rightarrow \frac{BE}{BA} = \frac{BH}{BM} \Rightarrow BE.BM = AB.BH$ (2)

Từ (1), (2)

d,

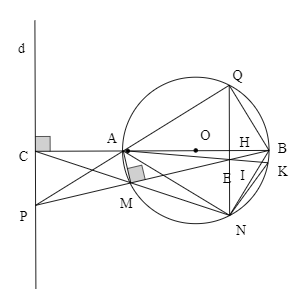
Kẻ Nx là tiếp tuyến của đường tròn ngoại tiếp tam giác NKE tại N (Nx thuộc nửa mặt phẳng bờ là đường thẳng NE chứa điểm A) (3)

Ta có:

tia Nx và NA trùng nhau.

NA là tiếp tuyến của đường tròn ngoại tiếp $\Delta NEK$ tại tiếp điểm N.

Gọi I là tâm đường tròn ngoại tiếp $\Rightarrow AN \perp NI$, mà $AN \perp BN$

N, I, B thẳng hàng.