Giải câu 19 Bài 3: Góc nội tiếp sgk Toán 9 tập 2 Trang 75

Câu 19: Trang 75 – SGK Toán 9 tập 2

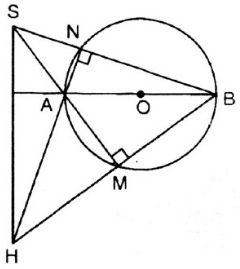
Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.

Bài làm:

Ta có: là góc nội tiếp chắn nửa đường tròn (O) => = $90^{\circ}$ => $BM\perp AM$ => $BM\perp SA$

Tương tự, có .

Như vậy BM và AN là hai đường cao của tam giác SAB mà BM cắt SA tại H

nên H là trực tâm => (đpcm)