Giải câu 33 Bài: Luyện tập sgk Toán 9 tập 2 Trang 80

Câu 33: Trang 80 – SGK Toán 9 tập 2

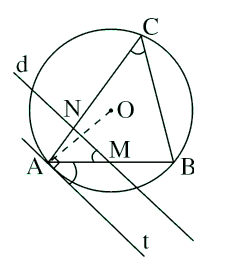
Cho A, B, C là ba điểm trên một đường tròn, At là tiếp tuyến của đường tròn tại A. Đường thẳng song song với At cắt AB tại M và cắt AC tại N. Chứng minh AB.AM = AC.AN.

Bài làm:

Vì: d // At (gt) => = $\widehat{MAt}$ (2 góc so le trong) (1)

Vì là góc tạo bởi tia tiếp tuyến At và dây cung AB của đường trong (O) và $\widehat{ACB}$ là góc nội tiếp chắn cung AB của đường tròn (O) nên

= $\widehat{ACB}$ (2)

Từ (1) (2) suy ra = $\widehat{ACB}$ (=$\widehat{BAt}$)

Xét và $\Delta ACB$ có:

chung, $\widehat{AMN}$ = $\widehat{ACB}$

=> (g.g)

=> = $\frac{AM}{AC}$ (cặp cạnh tương ứng tỉ lệ)

=> (đpcm)