Giải câu 2 trang 84 sách toán VNEN lớp 8 tập 2

Câu 2: Trang 84 sách VNEN 8 tập 2

Cho ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB và AC.

a) Chứng minh rằng: AEF ABC.

b) Cho AH = 4,8cm; BC = 10cm. Tính SAEF?

c) Lấy điểm I đối xứng với H qua AB. Từ B kẻ đường vuông góc với BC cắt AI ở K. Chứng minh rằng KC, AH, EF đồng quy tại một điểm.

Bài làm:

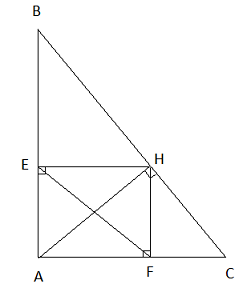
a) Gọi giao điểm của EF và AH là I

Ta có: + $\widehat{EAH}$ = ${90}^{\circ }$ (1)

Mặt khác: + $\widehat{AFE}$ = ${90}^{\circ }$ (2)

Tứ giác AEHF là hình chữ nhật nên: = $\widehat{EAH}$ (3)

Từ (1), (2),(3) suy ra: = $\widehat{AFE}$

Tương tự ta có: = $\widehat{AEF}$

Suy ra AEF $\sim$ ACB.

b) Tứ giác AEHF là hình chữ nhật nên AH = EF

Ta có tính chất: Tỉ lệ diện tích hai tam giác bằng bình phương tỉ lệ đồng dạng của hai tam giác đó

Tỉ lệ đồng dạng của AEF và ABC là:

= $\frac{AH}{BC}$ = $\frac{4,8}{10}$ = $\frac{12}{25}$

Suy ra = $\frac{144}{625}$

S ABC = $\frac{1}{2}$.AH.BC = 24 $c{m}^2$

Suy ra S AEF = $\frac{144}{625}$.24 = $\frac{3456}{625}$ $c{m}^2$