Giải toán VNEN 8 bài 6: Trường hợp đồng dạng thứ hai
Giải bài 6: Trường hợp đồng dạng thứ hai - Sách VNEN toán 8 tập 2 trang 68. Phần dưới sẽ hướng dẫn trả lời và giải đáp các câu hỏi trong bài học. Cách làm chi tiết, dễ hiểu, Hi vọng các em học sinh nắm tốt kiến thức bài học.
A. HOẠT ĐỘNG KHỞI ĐỘNG
1. a) Cho hai tam giác ABC và DEF có các kích thước như trong hình 37.
- So sánh các tỉ số: 
và $\frac{AC}{DF}$.
- Đo các đoạn thẳng BC, EF. Tình tỉ số , so sánh với các tỉ số trên và dự đoán sự đồng dạng của hai tam giác ABC và DEF.
b) Điền vào chỗ trống (...) để hoàn thiện lời giải.
Ta có: = $\frac{4}{8}$ = $\frac{.....}{.....}$; $\frac{AC}{DF}$ = $\frac{.....}{.....}$ = $\frac{.....}{.....}$; = $\frac{AC}{DF}$ = $\frac{.....}{.....}$.
- Học sinh đo và tính = $\frac{.....}{.....}$
- Suy ra = $\frac{AC}{DF}$ = $\frac{BC}{EF}$ = $\frac{1}{2}$.
Vậy ABC $\sim $ DEF.
Trả lời:
Ta có: = $\frac{4}{8}$ = $\frac{1}{2}$; $\frac{AC}{DF}$ = $\frac{3}{6}$ = $\frac{1}{2}$; = $\frac{AC}{DF}$ = $\frac{1}{2}$.
- Học sinh đo và tính = $\frac{1}{2}$
- Suy ra = $\frac{AC}{DF}$ = $\frac{BC}{EF}$ = $\frac{1}{2}$.
Vậy ABC $\sim $ DEF.
B. HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
2. c) * Vì sao ABC và PQR không đồng dạng với nhau?
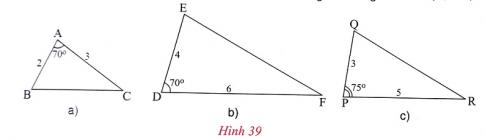
Trả lời:
ABC và PQR có $\frac{AB}{PQ}$ = $\frac{2}{3}$; $\frac{AC}{PR}$ = $\frac{3}{5}$
Suy ra: $\neq $ $\frac{AC}{PR}$
Vậy ABC và PQR không đồng dạng với nhau.
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Kiến thức thú vị
C. HOẠT ĐỘNG LUYỆN TẬP
Câu 1: Trang 71 sách VNEN 8 tập 2
a) Vẽ tam giác ABC có = $50^{\circ}$, AB = 5cm, AC = 7,5cm.
b) Lấy trên các cạnh AB, AC lần lượt hai điểm D, E sao cho AD = 3cm, AE = 2cm. Hai tam giác AED và ABC có đồng dạng với nhau? Vì sao?
Hướng dẫn:
- Vẽ hình (theo yêu cầu đề ra) (h.40).
- Hai tam giác ABC và AED có góc A chung.
So sánh các tỉ số và $\frac{AD}{AC}$ rồi rút ra kết luận.
Câu 2: Trang 71 sách VNEN 8 tập 2
Cho góc ( $\neq $ $180^{\circ}$) . Trên tia Ox lấy hai điểm A và B sao cho OA = 4cm, OB = 12cm. Trên tia Oy lấy hai điểm C và D sao cho OC = 6cm, OD = 8cm.
a) Chứng minh hai tam giác OCB và OAD đồng dạng.
b) Gọi giao điểm của các cạnh AD và BC là I, chứng minh rằng hai tam giác IAB và ICD có các góc bằng nhau từng đôi một.
D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNG
Câu 1: Trang 71 sách VNEN 8 tập 2
Đố em! Còn trường hợp đồng dạng nào của hai tam giác nữa?
Câu 2: Trang 71 sách VNEN 8 tập 2
Cho ABC vuông tại A và A'B'C' vuông tại A'. Nếu ta có $\frac{AB}{A'B'}$ = $\frac{AC}{A'C'}$ thì hai tam giác trên có đồng dạng với nhau không? Chứng minh.
Chú ý: Đây là một tính chất về một trường hợp đồng dạng của tam giác vuông.
Câu 3: Trang 71 sách VNEN 8 tập 2
Chứng minh rằng nếu hai tam giác đồng dạng thì tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.
Lớp 8