Giải câu 3 trang 114 toán VNEN 9 tập 2

Câu 3: Trang 114 toán VNEN 9 tập 2

Cho nửa đường tròn đường kính AB và điểm C di động trên cung AB. Lấy AC làm cạnh, vẽ tam giác đều ACD sao cho D và B là hai điểm khác phía so với đường thẳng AC. Gọi E là giao điểm của CD với cung AB. Gọi M là trung điểm của đoạn thẳng DC. Chứng minh rằng: Khi điểm C di động trên cung AB thì điểm M thuộc nửa đường tròn đường kính AE.

Hướng dẫn: Xem hình 101

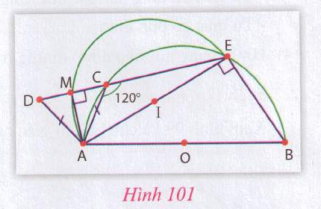
Theo giả thiết ta có nên $\widehat{ACE}={120}^{\circ }$ mà ACEB là tứ giác nội tiếp nên $\widehat{ABE}={60}^{\circ }$.

Do A, B cố định, (không đổi) nên điểm E cố định.

Theo giả thiết ACD là tam giác đều và M là trung điểm của đoạn DC nên , hay $\widehat{{90}^{\circ }}$.

Như vậy, do điểm M di động nhưng luôn nhìn đoạn thẳng AE

Bài làm:

Theo giả thiết ta có nên $\widehat{ACE}={120}^{\circ }$ mà ACEB là tứ giác nội tiếp nên $\widehat{ABE}={60}^{\circ }$.

Do A, B cố định, (không đổi) nên điểm E cố định.

Theo giả thiết ACD là tam giác đều và M là trung điểm của đoạn DC nên , hay $\widehat{{90}^{\circ }}$.

Như vậy, do điểm M di động nhưng luôn nhìn đoạn thẳng AE một góc không đổi nên M thuộc nửa đường tròn đường kính AE khi C di động.