Giải câu 3 trang 126 toán VNEN 9 tập 1
D. HOẠT ĐỘNG VẬN DỤNG
Câu 3: Trang 126 sách VNEN 9 tập 1
Cho đường tròn (O) và (O') cắt nhau tại A và B. Từ A kẻ lần lượt các tiếp tuyến với (O) và (O'), các tiếp tuyến này cát đường tròn (O) và (O') lần lượt tại D và C. Gọi I là trung điểm của OO'. Lấy K sao cho I la trung điểm của AK.
a) Chứng minh OO'//KB và KB ![]() AB.
AB.
b) Chứng minh tứ giác OAO'K là hình bình hành.
c) Chứng minh ![]() KAD và
KAD và ![]() KAC cân.
KAC cân.
d) Lấy E đối xứng với A qua B. Chứng minh bốn điểm A, C, E, D cùng nằm trên một đường tròn.
Bài làm:
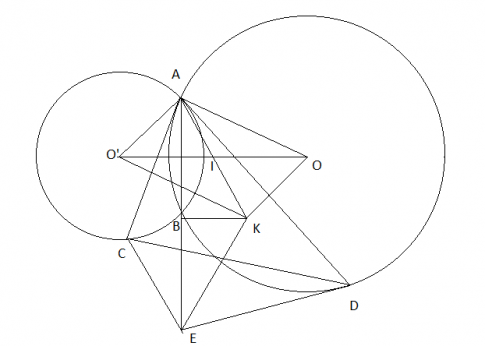
a) Ta có: AB có trung trực là OO'
![]() IA = IB = IK
IA = IB = IK ![]() $\Delta $ ABK vuông tại B
$\Delta $ ABK vuông tại B
![]() AB $\perp $ BK mà AB $\perp $ OO'
AB $\perp $ BK mà AB $\perp $ OO' ![]() OO' // BK.
OO' // BK.
b) Tứ giác OAO'K có hai đường chéo cắt nhau tại trung điểm của mỗi đường ![]() tứ giác OAO'K là hình bình hành
tứ giác OAO'K là hình bình hành
c) Ta có: OK//O'A và O'A ![]() AD $\Rightarrow $ OK
AD $\Rightarrow $ OK ![]() AD
AD
![]() OK là trung trực của AD
OK là trung trực của AD ![]() KA = KD hay tam giác KAD cân
KA = KD hay tam giác KAD cân
Tương tự ta chứng minh được O'K là trung trực của AC ![]() KA = KC hay tam giác KAC cân
KA = KC hay tam giác KAC cân
d) Từ câu a ta được AB ![]() BK, mặt khác AB = BE
BK, mặt khác AB = BE
![]() $\Delta $AKE cân
$\Delta $AKE cân ![]() KE = KA
KE = KA
Từ câu c ta được KA = KD = KC
![]() KA = KD = KC = KE hay bốn điểm A, C, E, D cùng nằm trên một đường tròn (đpcm).
KA = KD = KC = KE hay bốn điểm A, C, E, D cùng nằm trên một đường tròn (đpcm).
Xem thêm bài viết khác
- Giải câu 1 trang 96 toán VNEN 9 tập 1
- Giải câu 3 trang 72 toán VNEN 9 tập 1
- Giải câu 4 trang 15 toán VNEN 9 tập 1
- Giải toán VNEN 9 bài 4: Tính chất đồng biến, nghịch biến của hàm số y = ax + b
- Giải câu 8 trang 34 toán VNEN 9 tập 1
- Giải câu 1 trang 93 toán VNEN 9 tập 1
- Giải câu 4 trang 61 toán VNEN 9 tập 1
- Giải câu 4 trang 85 toán VNEN 9 tập 1
- Giải câu 2 trang 13 sách toán VNEN lớp 9 tập 1
- Giải câu 3 trang 52 toán VNEN 9 tập 1
- Giải toán VNEN 9 bài 2: Quan hệ giữa đường kính và dây cung của đường tròn
- Giải câu 3 trang 111 toán VNEN 9 tập 1











