Giải câu 3 trang 101 toán VNEN 9 tập 1

Câu 3: Trang 101 sách VNEN 9 tập 1

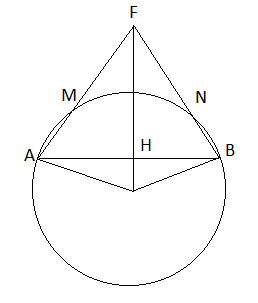
Cho hình 95. Trên đường tròn (O) lấy hai dây AM và BN bằng nhau (M và N nằm trên cùng một nửa mặt phẳng bờ là đường thẳng AB). Hai đường thẳng AM và BN cắt nhau tại F. Chứng minh rằng:

a) OF là phân giác của góc AOB.

b) OF vuông góc với AB.

Bài làm:

a) Theo bài ra vì AM và BN bằng nhau nên O cách đều hai đoạn thẳng AM và BN

O nằm trên đường phân giác của góc AOB hay OF là phân giác của góc AOB (đpcm).

b) Nối AB cắt OF tại H

Xét AHO và BHO có:

HO chung, OA= OB, = $\widehat{BOH}$

$\mathrm{\Delta }$AHO = $\mathrm{\Delta }$BHO (c.g.c)

$\widehat{AHO}$ = $\widehat{BHO}$

Mặt khác + $\widehat{BHO}$ = ${180}^{\circ }$

$\widehat{AHO}$ = $\widehat{BHO}$ = ${90}^{\circ }$ hay OF $\perp$ AB (đpcm)