Giải câu 4 đề 12 ôn thi toán lớp 9 lên 10
Bài 4: (3,5 điểm)
1. Từ điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AD, AE (D, E là các tiếp điểm).
Vẽ cát tuyến ABC của đường tròn (O) sao cho điểm B nằm giữa hai điểm A và C; tia AC nằm giữa hai tia AD và AO. Từ điểm O kẻ ![]() tại I.
tại I.
a. Chứng minh năm điểm A, D, I, O, E cùng nằm trên một đường tròn.
b. Chứng minh IA là tia phân giác của ![]() và $AB.AC=AD^{2}$
và $AB.AC=AD^{2}$
c. Gọi ![]() và $F$ lần lượt là giao điểm của $ED$ với $AC$ và $OI$. Qua điểm $D$ vẽ đường thẳng song song với $EI$ cắt $OF$ và $AC$ lần lượt tại $H$ và $P$. Chứng minh $D$ là trung điểm của $HP$.
và $F$ lần lượt là giao điểm của $ED$ với $AC$ và $OI$. Qua điểm $D$ vẽ đường thẳng song song với $EI$ cắt $OF$ và $AC$ lần lượt tại $H$ và $P$. Chứng minh $D$ là trung điểm của $HP$.
2. Một hình trụ có diện tích xung quanh ![]() và chiều cao là $h=7(cm)$. Tính thể tích của hình trụ đó.
và chiều cao là $h=7(cm)$. Tính thể tích của hình trụ đó.
Bài làm:
Hình vẽ:
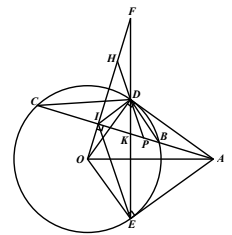
![]() ($OI\perp AC$ tại I)
($OI\perp AC$ tại I)
![]() (AD là tiếp tuyến của đường tròn (O) tại D).
(AD là tiếp tuyến của đường tròn (O) tại D).
![]() (AE là tiếp tuyến của đường tròn (O) tại E)
(AE là tiếp tuyến của đường tròn (O) tại E)
Vậy năm điểm A, D, I, O, E cùng nằm trên đường tròn đường kính AO (đpcm).
Xét đường tròn đường kính AO có:
![]() (các góc nội tiếp cùng chắn AD=AE)
(các góc nội tiếp cùng chắn AD=AE)
=> Tia IA là tia phân giác của ![]()
Xét (O) có ![]() (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn BD).
(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn BD).
Xét ![]() và $\Delta ADB$ có $\widehat{DAC}$ chung, $\widehat{ACD}=\widehat{ADB}$
và $\Delta ADB$ có $\widehat{DAC}$ chung, $\widehat{ACD}=\widehat{ADB}$
Do đó ![]() # $\Delta ADB$ (g.g)
# $\Delta ADB$ (g.g)
![]() (các cạnh tương ứng tỉ lệ).
(các cạnh tương ứng tỉ lệ).
![]() (đpcm)
(đpcm)
Vì IA là tia phân giác của ![]() mà $IA\perp IF$
mà $IA\perp IF$
=>IF là tia phân giác ngoài tại đỉnh I của ![]()
![]()
Xét ![]() có HD//IE $\Rightarrow \frac{HD}{IE}=\frac{FD}{FE} (2)$
có HD//IE $\Rightarrow \frac{HD}{IE}=\frac{FD}{FE} (2)$
Xét ![]() có DP//IE $\Rightarrow \frac{DP}{IE}=\frac{DK}{KE} (3)$
có DP//IE $\Rightarrow \frac{DP}{IE}=\frac{DK}{KE} (3)$
Từ (1), (2) và (3) suy ra ![]()
Vậy điểm D là trung điểm của đoạn thẳng HP.
2. Bán kính đáy của hình trụ ![]() .
.
Thể tích của hình trụ ![]()
Xem thêm bài viết khác
- Ôn thi lên lớp 10 môn Toán Chuyên đề Phương pháp đại số trong bài toán diện tích đa giác
- Giải câu 5 đề 7 ôn thi toán lớp 9 lên 10
- Đề thi thử vào 10 môn Toán trường THCS Ái Mộ năm 2022 Đề thi thử vào lớp 10 môn Toán 2022
- Đáp án đề thi vào lớp 10 môn Toán Nghệ An năm 2022 Đề thi môn Toán vào lớp 10 tỉnh Nghệ An năm 2022
- Đáp án đề thi vào lớp 10 môn Toán Sơn La năm 2022 Đề thi môn Toán vào lớp 10 tỉnh Sơn La năm 2022
- Giải câu 4 đề 7 ôn thi toán lớp 9 lên 10
- Giải câu 3 đề 1 ôn thi toán lớp 9 lên 10
- Đề thi tuyển sinh lớp 10 chuyên Toán trường Phổ thông Năng khiếu năm 2022 Đề thi vào 10 chuyên Toán năm 2022
- Đề thi tuyển sinh lớp 10 chuyên Toán Phú Yên năm 2022 Đề thi vào 10 chuyên Toán Phú Yên năm 2022
- Giải câu 1 đề 3 ôn thi toán lớp 9 lên 10
- Đề thi thử Toán vào 10 tỉnh Thái Nguyên năm 2022 Đề thi thử vào lớp 10 môn Toán 2022
- Lời giải bài 1 chuyên đề Vận dụng bất đẳng thức Côsi để tìm cực trị











