Giải câu 4 trang 102 toán VNEN 9 tập 2

C. Hoạt động luyện tập

Câu 4: Trang 102 toán VNEN 9 tập 2

Gọi (O; R) là đường tròn đi qua ba đỉnh của tam giác ABC. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CA, AB. OM cắt cung nhỏ BC tại D, ON cắt cung nhỏ CA tại E, OP cắt cung nhỏ AB tại F. Gọi I là giao điểm của AD và CF.

a) Chứng minh rằng: Hai dây AD và EF vuông góc với nhau.

b) Chứng minh rằng: DC = DI.

Bài làm:

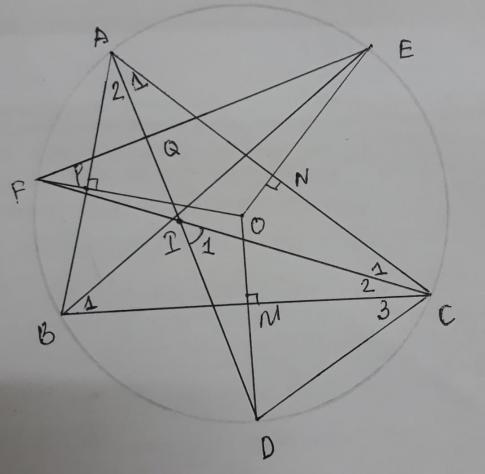
a) Gọi Q là giao điểm của AD và EF.

Ta có: M, N, P lần lượt là trung điểm của BC, AC và AB nên D, E, F lần lượt là điểm chính giữa của các cung BC, cung AC, cung AB.

AD, BE, CF lần lượt là tia phân giác của các góc $\widehat{BAC};\;\widehat{ABC};\;\widehat{ACB}$

• Xét cung nhỏ AF: (1)

• Xét cung nhỏ DE:

cung DE = cung DC + cung CE.

(2)

Từ (1) và (2) (tổng ba góc trong tam giác)

Lại có: là góc trong của (O; R) $\Rightarrow \widehat{AQF} = \frac{1}{2}(sd DE + sd AF) = \frac{180^\circ}{2} = 90^\circ$

AD vuông góc với EF tại Q

b) Xét tam giác có $\widehat{I_1} = \widehat{A_1} + \widehat{C_1}$ (tính chất góc ngoài). (1)

Ta có:

Mà (Góc nội tiếp cùng chắn cung BD) $= \widehat{A_1} $ (Do AD là tia phân giác góc BAC)

(Do CF là tia phân giác góc ACB)

(2)

Từ (1) và (2) suy ra: Tam giác IDC cân tại D, hay ID = IC.