Giải câu 4 trang 98 toán VNEN 8 tập 1

Câu 4: Trang 98 toán VNEN 8 tập 1

Dựa vào tính chất của hình chữ nhật, chứng tỏ rằng: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy và ngược lại.

Bài làm:

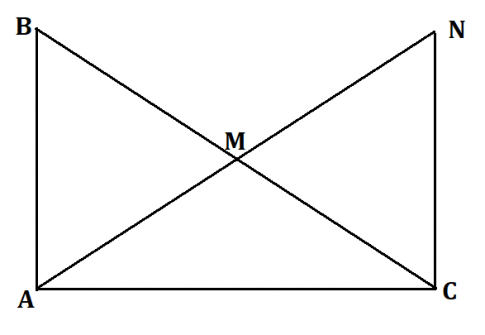
Xét tam giác ABC có M là trung điểm của BC.

Trên tia đối của tia MA lấy điểm N sao cho MN = MA.

Xét MAB và MNC, có:

• BM = CM
• MA = MN
• = $\widehat{NMC}$ (đối đỉnh)

$\Delta$MAB = $\Delta$MNC (c.g.c)

NC = AB và $\widehat{MBA}$ = $\widehat{MCN}$

a) Do = $\widehat{MCN}$ nên AB // NC $\Rightarrow$ $\widehat{BAC}$ + $\widehat{ACN}$ = 180$^{0}$.

Nếu = 90$^{0}$ thì $\widehat{ACN}$ = 90$^{0}$.

Xét ABC và CNA, có:

• AC chung
• AB = NC (cmt)
• = $\widehat{ACN}$ (cmt)

$\Delta$ABC = $\Delta$CNA (c.g.c)

AN = BC AM = 12BC (đpcm).

b) Có: AM = 12AN. Nếu AM = 12BC thì AN = BC.

Xét ABC và CNA, có:

• AC chung
• AB = NC (cmt)
• AN = BC (cmt)

$\Delta$ABC = $\Delta$CNA (c.c.c) $\widehat{BAC}$ = $\widehat{ACN}$

Mà + $\widehat{ACN}$ = 180$^{0}$ nên = 90$^{0}$ (đpcm).