Giải câu 3 trang 114 toán VNEN 8 tập 1

Câu 3: Trang 114 toán VNEN 8 tập 1

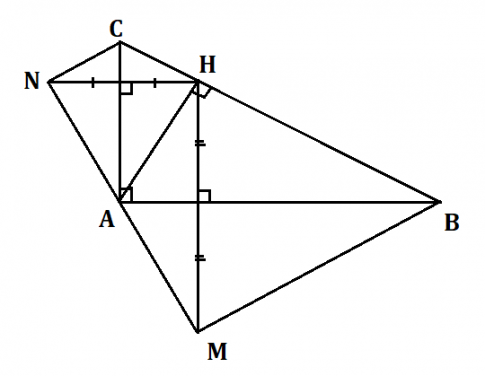
Cho tam giác ABC vuông tại A, có đường cao AH. Gọi M là đối xứng của H qua AB, gọi N là đối xứng của H qua AC. Chứng minh rằng:

a) AM = AN;

b) M là đối xứng của N qua A;

c) MHN là tam giác vuông tại H;

d) MN vuông góc CN;

e) BMNC là hình thang vuông.

Bài làm:

a) Vì M đối xứng với H qua AB AH = AM

Và N đối xứng với N qua AC AH = AN

Do đó: AM = AN (4) (= AH).

b) Xét ABM và ABH, có:

AM = AH (H đối xứng với M qua AB)

BM = BH (H đối xứng với M qua AB)

AB chung

$\mathrm{\Delta }$ABM = $\mathrm{\Delta }$ABH (c−c−c).

$\widehat{MAB}$ = $\widehat{BAH}$ (1)

Tương tự, ta có: ACN = ACH $\Rightarrow$ $\widehat{NAC}$ = $\widehat{CAH}$ (2)

Mà + $\widehat{CAH}$ = 90${}^0$ (3)

Từ (1), (2) và (3) $\widehat{MAB}$ + $\widehat{BAH}$ + $\widehat{NAC}$ + $\widehat{CAH}$ = 2$\widehat{BAH}$ +2$\widehat{HAC}$ = 2.90${}^0$ = 180${}^0$

M, N, A thẳng hàng. (5)

Từ (4) và (5) M đối xứng với N qua A.

c) Xét MHN, có: AH = MA = NA (cmt)

AH = $\frac{MA+NA}{2}$ = $\frac{MN}{2}$ $\mathrm{\Delta }$MHN vuông tại H.

d) Do ACH = ACN (cmt) $\Rightarrow$ $\widehat{AHC}$ = $\widehat{ANC}$ = 90${}^0$ $\Rightarrow$ MN $\perp$ CN.

e) Do ABM = ABH (cmt) $\Rightarrow$ $\widehat{AMB}$ = $\widehat{AHB}$ = 90${}^0$.

Xét tứ giác BMNC, có: = $\widehat{MNC}$ = 90${}^0$

Mà hai góc này ở vị trí so le trong

BMNC là hình thang

Mà hai góc đó cùng bằng 90

BMNC là hình thang vuông.